Analyse Combinatoire

Détails
Affichages : 38376

Vote utilisateur: 3 / 5

Etoiles activesEtoiles activesEtoiles activesEtoiles inactivesEtoiles inactives
 

Histoire de l'analyse combinatoire : Arrangements et Combinaisons

La combinatoire, appelée aussi analyse combinatoire, étudie les configurations de collections finies d'objets ou les combinaisons d'ensembles finis, et les dénombrements.

 

Arrangements

  • Définition ([EscoJ]  p 177)
    Soit A un ensemble non vide. On appelle arrangement de p éléments de A toute p-liste (a1;...;ap) d'éléments deux à deux distincts.

  • Propriété
    On note  \(A_n^p\) le nombre d'arrangements de p éléments d'un ensemble de n éléments
    et l'on a pour 0 ≤ p ≤ n,

$$A_n^p=n\times (n-1) \times \cdots \times (n-p+1)=\dfrac{n!}{(n-p)!}$$

 

Combinaisons

  • Définition ([EscoJ]  p 179).
    Soit E un ensemble de cardinal n. On appelle combinaison de p éléments de E toute partie de E de cardinal p.

  • Propriété
    On note \(C_n^p\) ou \(\begin{pmatrix}{n}\\{p}\end{pmatrix}\) le nombre de combinaisons de p éléments d'un ensemble de n éléments
    et l'on a pour 0 ≤ p ≤ n :

  • Propriétés
    Pour tout n et p tels que 1 ≤ p ≤ n,

cnp

cn0

cnn-p

pcnp

cnp+

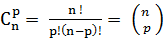
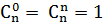
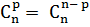
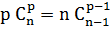
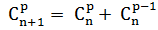
Histoire. [Bourb] p 65

Les problèmes généraux d"Analyse combinatoire" ne sont abordés que lors des derniers siècles de l'Antique classique.

  • La formule \(\begin{pmatrix}{n}\\{p}\end{pmatrix} = \dfrac{n(n-1)}{2}\)    apparait au 3e siècle de notre ère.

  • Le mathématicien hindou BHASKARA (1114 - 1185) connaît lui la formule générale pour Cnp.

  • Une étude plus approfondie est effectuée par GERSONIDE (1288 - 1344). C'est lui qui obtient la formule de récurrence permettant de calculer le nombre d'arrangements Anp et le nombre de permutations de n éléments.

    Il propose des règles équivalentes aux relations :

$$ C_n^p = \dfrac{A_n^p}{p!} ~~~~\text{et}~~~~\begin{pmatrix}{n}\\{p}\end{pmatrix}=\begin{pmatrix}{n}\\{n-p}\end{pmatrix}$$

  • Cependant ce manuscrit est ignoré de ses contemporains et ses résultats ne sont retrouvés que peu à peu aux siècles suivants.
  • Le mathématicien italien CARDAN Girolamo (1501-1576) démontre que le nombre de parties non vides d'un ensemble de n éléments est 2n - 1.

  • Par la suite, les français PASCAL Blaise (1623-1662) et FERMAT Pierre de (1601-1665) fondent le calcul des probabilités et retrouvent parallèlement l'expression :

cnp

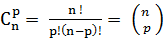
  • La formule du binôme.
    La relation entre ces nombres et la formule du binôme est observée pour la première fois par PASCAL Blaise (1623-1662) mais il semble avéré que celle-ci soit déjà connue des arabes au 13ème siècle et des chinois au 14ème siècle.
    Elle est par ailleurs retrouvée en Occident au début du 16ème siècle avec la méthode de calcul par récurrence dite du "triangle de Pascal" ou "triangle arithmétique"..

 

Notations

=> voir histoire des symboles

 

 


Articles Connexes