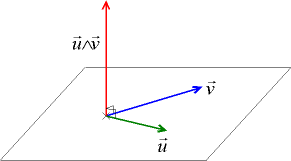
Le produit vectoriel.
Approche Historique.
Histoire. [Dieudo]p106 et [Audi] p 159, p 163
Le produit vectoriel prend naissance avec "l'invention" des quaternions en 1843, par le mathématicien irlandais HAMILTON William Rowan (1805-1865). Le mathématicien américain GIBBS Josiah Willard (New Haven 1839 - 1903) simplifie cet outil et définit le produit scalaire et le produit vectoriel dans une théorie appelée l'analyse vectoriel.
Parallèlement à l'américain GIBBS, le mathématicien anglais HEAVISIDE Oliver (1850-1925) introduit l'analyse vectorielle. Trouvant malcommode l'utilisation des quaternions en physique, il sépare du produit de 2 quaternions purs, la partie réelle et la partie vectorielle. Cela donnera au signe près le produit scalaire et le produit vectoriel.
L'approche du mathématicien allemand GRASSMANN Hermann (1809-1877) est elle plus géométrique.
En 1844, GRASSMANN expose dans Die lineale Ausdehnungslehre ein neuer Zweig der Mathematikpropose l'introduction des notions fondamentales d'algèbre linéaire. GRASSMANN développe ainsi la notion de produit extérieur (produit vectoriel) et invente l'algèbre extérieure.
Son idée est d'étendre le calcul des vecteurs à des grandeurs orientées de dimension quelconque. Il considère alors un produit extérieur (maintenant vectoriel) de deux vecteurs comme l'aire orientée du parallélogramme construit sur ces deux vecteurs.
Il définit alors la linéarité de ce produit et généralise son produit de 2 vecteurs à celui de p-vecteurs considéré comme le volume orienté à p dimensions du parallélotope construit sur ces vecteurs.
Il se heurte à des difficultés lorsqu'il veut additionner ces p-vecteurs.
En 1862, GRASSMANN il adopte le point de vue de HAMILTON. Il part alors d'une base (e1,..,en) de IRn et définit son produit extérieur d'abord sur les ei puis l'étend aux vecteurs par linéarité.
Cette algèbre extérieure restera tout de même confidentielle jusqu'aux travaux des mathématiciens français POINCARÉ Jules Henri (1854-1912) et de CARTAN Elie Joseph (1869-1951) en géométrie différentielle.
Cours.
- Définition du Produit vectoriel dans E espace euclidien de dimension 3.
- Propriétés.
- Produit mixte. (Généralisable dans un ev de dimension n).
- Généralisation du produit vectoriel.
- Propriétés différentielles et de continuité.
1°) Définition du Produit vectoriel dans E espace euclidien de dimension 3.
Dans une base orthonormée
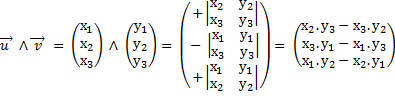
Remarque : Notez la permutation circulaire permettant de passer d'une ligne à l'autre !
2°) Propriétés.
-
L’application produit vectoriel est bilinéaire et antisymétrique
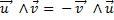
-
La famille (u,v) est liée ⇔
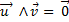
-
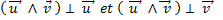
-
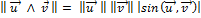
-
L’aire du parallélogramme construit sur u et vest égale à :
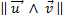
-
Double produit vectoriel : (attention, il faut que les coordonnées des vecteurs commutent !)
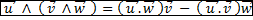
-
Identité de Jacobi : du mathématicien allemand JACOBI Carl Gustav Jacob (1804-1851)
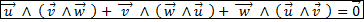
3°) Produit mixte. (Généralisable dans un ev de dimension n)
L’application produit mixte est antisymétrique et trilinéaire.
Théorème de Hadamard :
Avec égalité si l’un des vecteurs est nul ou si (u,v,w ) est une BON .
4°) Généralisation du produit vectoriel. [Ladeg p 125]
Pour tout couple de vecteurs (u,v) de l’espace vectoriel euclidien orienté de dimension 3, Il existe un unique vecteur V tel que pour tout vecteur w , on a :
.
Ce vecteur V est appelé produit vectoriel de u et v.
Remarque : Cette définition est généralisable en dimension n pour n - 1 vecteur (n>2)
5°) Propriétés différentielles et de continuité.
5.a : Continuité des applications multilinéaires en dimension finie.
- Théorème. [Monier2p68]
Soit pour k entier, Ek et F des IK-ev.
Si les Ek sont de dimensions finies, alors toute application multilinéaire de ∏Ek dans F est continue.- Conséquences : Pour E de dimension finie.
Pour y fixé, l’application de E → IK qui : x → < x , y > est continue (car linéaire).
Pour y fixé, l’application de E → E qui : x →
est continue (car lineaire).
Les applications normes, produit scalaire, produit mixte et produit vectoriel sont continues.
5.b : Dérivée et différentielle.
- Fonctions bilinéaires : [SoroAn]p354
(f bilinéaire de IRp × IRn dans F ) ⇒ ( f est différentiable) et
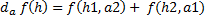
- Conséquences.
Le produit scalaire et le produit vectoriel sont différentiables et :