Plan d'Argand-Cauchy.

Le plan d'Argand-Cauchy est la représentation géométrique des nombres complexes par un plan muni d'un repère orthonormé.
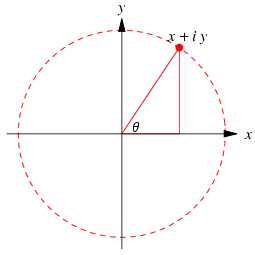
Le nombre complexe z = a + ib étant identifié au point M de coordonnées (a ; b) dans un repère orthonormal du plan par une relation biunivoque.

Histoire.

Le mathématicien suisse Jean-Robert Argand (1768-1822) introduit en 1806 la configuration plane des nombres complexes.
Cette dernière est faite avant lui par Wessel (1745-1818) dans l'article "Sur la représentation analytique d'une direction" qui associe à tout nombre complexe un vecteur d'origine 0 et interprète sur ces vecteurs les opérations élémentaires sur les complexes. Cette publication passe cependant inaperçue à l'époque et les travaux de Wessel ne seront retrouvés qu'en 1897.

Il failli en être de même du traité d'Argand " Essai sur une manière de représenter les quantités imaginaires" publié à Paris en 1806. Il y expose sa façon de représenter le complexe i comme une opération de rotation d'un angle droit autour de l'origine et il interprète géométriquement les opérations sur les nombres complexes.
Cet essai tombe aussi dans l'oubli jusqu'à ce qu'un certain Joseph François FRANÇAIS (7 avril 1768 à Saverne (Bas-Rhin), mort le 30 octobre 1810 à Mayence), professeur à l'école impériale de l'Artillerie et du Génie, qui développe la même notion et y ajoute une notation exploitable.
Il reconnait que l'idée n'est pas de lui et en recherche son auteur. Il s'ensuit alors une correspondance entre les deux hommes,
Ces conceptions furent donc diffusées à la suite d'une polémique à ce sujet en 1813-1814 dans "Les annales de Gergonne" (première revue mathématique [1]).

Par la suite Gauss (1777-1855) et Cauchy (1789-1857) compléteront les recherches effectuées et adopteront cette représentation.

Bibliographie.

• Références : [HaSu] p 15 et [Dieudo] p 132
• [1] Remarque : Les annales de Gergonne sont disponibles sur le site NUMDAM.