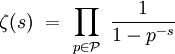RIEMANN Georg Friedrich Bernhard

Né à Breselenz (État de Hanovre) en 1826 - Mort à Selasca (Italie) 1866 , Allemagne.

Riemann, un géant.

Né à Breselenz (Allemagne), Riemann, étudiant à Gottingen et à Berlin, passa son doctorat à Gottingen, en 1851, s'y fit habiliter en 1853, y enseigna et succéda, en 1859, à Dirichlet dans la chaire de mathématiques. Atteint de tuberculose à partir de 1862, il est mort lors d'un troisième voyage en Italie.
Bien que mort très jeune (oui à 40 ans), son influence est immense et son oeuvre gigantesque.

1. Sa thèse de 1851.

Dans sa thèse de 1851, il étudie les fonctions dites multivaluées de variables complexes (fonctions qui peuvent avoir plusieurs images) qui préoccupent les mathématiciens.

Par exemple :  f(z) = √z + 1 qui a deux images pour tout nombre comple non nul.

Ces fonctions apparaisent en fait quand on cherche au siècle précédent une interprétation des logarithmes complexes. Elle donne lieu à une controverse célèbre entre les géants de l'époque (Jean BERNOULLI, LEIBNIZ, EULER). [Dieudo] p 126

=> Pour en savoir plus : Histoire de la notion de fonction.

Toujours dans cette thèse, il développe les fonctions harmoniques, démontre la formule dite de Green Riemann et, étudiant le problème de DIRICHLET, il démontre le principe du maximum et du prolongement analytique.
Il y introduit aussi, lla notion des surfaces qui portent son nom, notamment les sphères de Riemann.

En 1857, il généralise la construction des surfaces de Riemann à des relations P(z ,z') = 0 où P est un polynôme irréductible. Il en sort ce qu'il nomme une fonction algébrique et il étudie les intégrales abéliennes.

2. Sa soutenance d'habilitation en 1857.

Riemann cherche à devenir Privatdozent, (Privat-docent). Cette distinction académique sert à désigner, dans plusieurs pays d'Europe, des enseignants qui ont écrit une habilitation, mais n'ont pas reçu une chaire d'enseignement ou de recherche.
Il présente son mémoire d'habilitation (Habilitationsvortrag) à l'université de Göttingen en 1854.

Ce mémoire, Sur la possibilité de représenter une fonction par une série trigonométrique ("Über die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe"), est publié en 1868 par son ami DEDEKIND (1831-1916).

Il eut un impacte considérable et fut traduit en français en 1873 par DARBOUX (1842-1917) et HOUEL.
DARBOUX écrivit d'ailleurs à HOUEL le 18 mars 1873 :

"Ce mémoire de Riemann est un chef-d'oeuvre semblable à ces vieux tableaux dont quelques parties en pleine lumière vous font regretter ce que le temps a détruit ou ce que l'auteur a négligé." [Dugac] p 142

Son exposé est révolutionnaire. Au lieu de définir le géométrie non euclidiennes en niant le cinquième postulat d'Euclide, il invente une métrique locale en utilisant la variation infinitésimale de la distance en fonction de celle des coordonnées.

Il pose ds² = ∑ g _i,j dx_i dx_j où (g _i,j ) est la matrice d'une forme quadratique définie positive (au lieu de ds² = ∑ dx_i²).

Il généralise la notion de courbure propre à GAUSS (1777-1855) ce qui permettra l'éclosion de la thérie de la relativité d'EINSTEIN.

Etude du mémoire de 1854. ^{[Dugac] p 143 et [Dieudo] p 259 et [HaSu] p 300}

• Il expose une analyse historique du développement des séries trigonométriques avant Fourier.
• Il propose une étude du mémoire de DIRICHLET (1805-1859) sur ces même séries trigonométriques et démontre un théorème sur les série commutativement convergentes.

Théorème : On peut permuter les termes d'une série numériques semi-convergente de telle façon que l'on obtienne une série convergent dont la somme est égale à un nombre réel quelconque donné à l'avance. [TisAgreg] ^p191

• On montre aussi que toute série réelle absolument convergente est commutativement convergente et la réciproque est vraie pour les séries réelles.
  [TisAgreg] ^p155
  
  
• Il expose alors les conditions pour qu'une fonction périodique puisse être représentée par une série trigonométrique :

1°) La fonction doit être généralement susceptible d'intégration.

2°) elle n'a pas un nombre infini de maximums et de minimums

• Afin d'élargir cette représentation à d'autres fonctions, il élabore une nouvelle théorie de l'intégrale :

Pour qu"une fonction bornée soit intégrable sur le segment [a;b], il faut et suffit qu'on puisse diviser [a;b] en intervalles tels que la somme des longueurs de ceux des intervalles dans lesquels l'oscillation est plus grande que ε, quel que soit ε > 0, soit aussi petite que l'on veut."

• Il montre que les fonctions monotones sont intégrables et donne même un exemple de fonction bornée, ayant une infinité dénombrable de discontinuités et intégrable. La recherche de ces fonctions particulières motivera nombre de mathématiciens (H.J. Smith en 1875, V. Voltera en 1881..)
  
  
• Remarques :
  Une fonction classique non intégrable au sens de Riemann est la fonction qui dans [a;b], vaut 1 si x est rationnel,et 0 sinon. cette fonction est appellée, fonction de DIRICHLET.
  
  Henri Lebesgue montre en 1904, qu'une fonction bornée est intégrable au sens de Riemann si et seulement si l'ensemble de ses points de discontinuité est de mesure nulle. [HaSu] p 209
  
  
• Riemann introduit alors une méthode révolutionnaire.
  
  Il considère la série f(x) = A₀ + A₁ + ... + A_n + .... où A₀ = a₀/2 et A_n = a_n.cos nx + b_n.sin nx (n entier > 0).
  Il suppose que les A_n tendent vers 0 (quand n → ∞) et intègre deux fois terme à terme sans justifier la légitimité de cette intégration, pour obtenir la série : F(x) = B + B'.x + A₀.x²/2 - A₁ - A₂/4 - A₃/9 -...
  
  Il montre alors que la série obtenue, est convergente et que la fonction F est continue.
  
  Bien évidemment, il manque l'hypothèse de convergence uniforme sur [a;b] de la série. 
  
  
• Il montre aussi que les coefficients de Fourier d'une fonction intégrable tendent vers zéro (Lemme de Riemann - Lebesgue) et donne une condition nécessaire et suffisante pour qu'une série trigonométrique ∑(a_n.cos nx + b_n.sin nx) converge lorsque les suite (a_n) et (b_n) convergent vers 0. (*)
  
  
• Il montre par un exemple qu'une fonction intégrable peut ne pas avoir de développement en série de Fourier mais ne parvient pas à donner une CNS d'existance de ce développement. [HaSu] p 300
  
  (*) Remarque : [AuCA] p 425
  Si les deux suites (an) et (bn) sont positives, décroissantes et de limites nulle, alors la série trigonométrique
  ∑(an.cos nx + bn.sin nx) converge simplement sur IR\2piZ, uniformément sur tout segment inclus dans cet ouvert.

=> Pour en savoir plus : Le lemme de Riemann - Lebesgue ou Théorème de Riemann.

Riemann et la théorie des nombres.

En 1859, Riemann, qui vient juste d'être nommé professeur à Göttingen et à l'Académie des Sciences de Berlin, publie un article, « Sur le nombre de nombres premiers inférieurs à une taille donnée ».

Il y définit et étudie la fonction zêta, en reprenant les travaux de Euler et en les étendant aux nombres complexes.

• La fonction Zêta (ou dzêta) (qu'il baptise ainsi dès 1857, [Hauch]^p222) est définie par :

C'est une fonction analytique complexe méromorphe définie, pour tout nombre complexe s tel que Re(s) > 1,

Il utilise cette fonction dans le but d'étudier la répartition des nombres premiers. La célèbre hypothèse de Riemann sur les zéros non triviaux de la fonction zêta, formulée dans cet article, n'est toujours pas démontrée et fait partie des fameux 23 problèmes de Hilbert (ainsi que des 7 problèmes du millénaire).

En effet, si P désigne l'ensemble des nombres premiers, on a la relation : (Pour une démonstration voir [KoMe] p 105)