Évolution de l'écriture d'une équation.
Si les babyloniens savaient déjà résoudre des équation du 2ème degré, le symbolisme utilisé a beaucoup évolué au cours des siècles comme le montre le tableau ci-dessous.
2x² - 5x = 23
| Diophante (vers 250) | 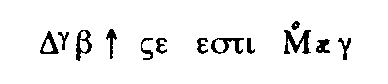 |
| Tartalia (1556) Pacioli (1494) |
Trouve moi un nombre dont le double du carré diminué de cinq fois lui-même fait vingt-trois |
| Van der Hoek (début du 16ème siècle) |
2 SC - 5 PN dit is ghelije 23 |
| Cardan(1545) | duo quad. m qumque reb. aequalis 23 |
| Rudolf, Stiffel (1577) Leon d'Anvers (1586) |
2 z aequatus 5x+23 |
| Gosselin (1577) | 2Q M 5L aequalia 23
Q :carré ("quarré") au 16ème |
| Bombelli (1572) | 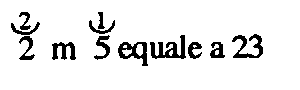 |
| Viète (1580) | 2Q - 5N aequatur 23 |
| Ramus (1586) Clavius (1608) |
2q - 5l aequatus sit 23 |
| Butéo (1559) | 2à M 5p = 23 |
| Girard (1629) Théorie des équations, il énonce le théorème de d'Alembert |
2(2) - 5(1) = 23(0) |
| Viète (1600) | 2aq 5a aeq. 23 |
| Harriot (1631) | 2aa 5a = 23 |
| Descartes (vers 1635) et dans "la géométrie" en 1637 |
2Aq - 5A égal à 23 2zz - 5z µ 23 |
| Herrigone (1634) | 2a2 ~ 5a z/z 23 |
| Et durant tout le 18ème siècle | 2xx - 5x = 23 |


