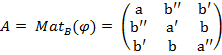Formes quadratiques, histoires et définition.
Définition.
Définition. [Gour2] p 225 , [MonAl2] p 119, [Hprepa] p97
Soit IK un corps de caractéristique différente de 2.
On appelle forme quadratique sur E, un IK-ev, toute application de la forme : q : E → IK telle que q(x) = φ ( x , x) où φ est une forme bilinéaire sur E.Propriété.
1°) Pour toute forme quadratique q sur E, il existe une unique forme bilinéaire symétrique φ telle que q(x) = φ ( x , x).
On la nomme forme polaire de q, et l'on a : φ ( x , y) = 1/2 . [ q(x+y) - q(x) - q(y) ] = 1/4 . [ q(x+y) - q(x-y) ]
2°) Soit φ une forme bilinéaire symétrique sur E², et B=(e1,..,en) une base de E.
On note Mat B (φ) = ( φ ( e1,ej) )
Alors si A = Mat B (φ), on a : φ ( x , y) = tX.A.Y et q(x) = tX.A.X (pour X = Mat B (x) et Y = Mat B (y) )
Par exemple
L'application q définie sur IR3 par q(x) = 3x² - 2y² + 8xy + 6yz - 4xz est une forme quadratique sur IR3
car c'est un polynôme homogène de degré 2 (en fonction des coordonnées de la base canonique). Alors :
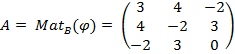
Histoire
Jean DIEUDONNE ([Dieudo]p64) considère qu'il n'y a pas véritablement de théorie algébrique des formes quadratiques au 18ème siècle (pas vraiment d'algèbre linéaire non plus).
En analyse.
En analyse, LAGRANGE Joseph Louis (1736-1813) étudie les extremums relatifs de fonctions à plusieurs variable.
Il construit une forme quadratique en réunissant les termes de dégré 2 dans le développement de TAYLOR de la fonction au voisinage du point.En dehors de cela, on ne rencontre au 18ème siècle que des formes quadratiques de 2 ou 3 variables. Avec les coniques et notamment la poursuite des travaux effectué par FERMAT Pierre de (1601-1665) , avec les quadriques étudiées par EULER(1707 - 1783) et avec les équations diophantiennes du second degré).
Les travaux d'EULER Leonhard (1707- 1783).
EULER Leonhard (1707- 1783) cherche par un changement d'axes rectangulaire à ramener l'équation de la quadrique à une forme plus simple (Ax² + By² + Cz² + D = 0).
Il montre que si l'équation initiale de la quadrique est ax²+a'y²+a''z² + 2byz+2b'zx+2b''xy+cx+c'y+c''z+d = 0, une telle réduction n'est possible que si : ab²+a'b'²+a''b''²-aa'a''-2bb'b'' ≠0.Ceci correspond au du déterminant de la matrice de la forme quadratique : q(x,y,z) = ax² + a'y² + a''z² + 2byz + 2b'zx + 2b''xy
On a det A = aa'a'' + 2bb'b'' - ab² - a'b'² - a''b''² (on peut appliquer la règle de SARRUS) et quand ce déterminant n'est pas nul, les coefficient A, B, C sont les valeurs propres de la matrice A.
Puis LAGRANGE retrouve un problème similaire en 1773 en étudiant le mouvement d'un corps solide.
Les travaux de CAUCHY Augustin-Louis (1789-1857)
Enfin CAUCHY en 1826 (pour préparer son enseignement à l'école politechnique) reprend ce problème de réduction d'une quadrique à ses axes. [DaDaPe] précise la problématique de CAUCHY.
CAUCHY étudie une quadrique (surface du second degré) dont le centre est pris comme origine.
Cette quadrique est d'équation : Ax² + By² + Cz² + 2Dyz + 2Ezx + 2Fxy = K.Cherchant à en déterminer les axes principaux, il obtient une équation exprimant qu'un certain déterminant Δ est nul.
![]()
Ce Δ constitue le polynôme caractéristique de la matrice de la forme bilinéaire associée à la forme quadratique.
Il démontre que les racines de ce polynôme (i.e. les valeurs propres de la matrice) sont réelles. Puis il montre que ce polynôme est indépendant de tout changement d'axex rectangulaires (i.e. les transformations semblables ont même valeurs propres).
Compléments.
En algèbre au 18ème siècle, l'objectif principal des mathématiciens est la recherche de transformations linéaires permettant de ramener des formes quadratiques (∑aii xi² + ∑aii aij.xi.xj , pour 1 ≤ i < j ≤ n ) à 2 ou 3 variables à des types simples.
On cherche donc à classes ces formes quadratiques par des invariants caractérisant ces formes réduites.
EULER Leonhard (1707- 1783) obtient en géométrie sa classification des quadriques, et LAGRANGE et GAUSS développe leur théorie des formes binaires en arithmétique (ax² + bxy + cy² = n, avec a,b,c,n, x et y entiers). ([Dieudo] p 97 et p 165)