Notions mathématiques, théorèmes et conjectures
Je vous présente les principales notions et théorèmes mathématiques en partant d'une approche historique.
Les notions suivies du symboles => sont développées.
Liens directs : A - I / J - L / M - Z
A.
Accumulation, point. (point d'accumulation)
Définition ( [Gour1] p 11)
Soit A une partie du IK-espace vectoriel E.
On dit que a ∈ E est un point d'accumulation de A si pour tout voisinage V de a,
(V ∩ A) est non vide et ( V ∩ A ) ≠ {a}. Soit :![]()
Histoire [Gour1] p 8
C'est le mathématicien allemand WEIERSTRASS Karl Theodor Wilhelm (1815-1897), vers 1860, qui donne la définition de la notion de point d'accumulation.
Il démontre que: tout ensemble de nombres réels infini borné admet au moins un point d'accumulation.
Ce résultat était auparavant admis.
Anneau
Histoire.
Le terme d'anneau est introduit par le mathématicien allemand HILBERT David (1862-1943) en 1897. [Dieudo] p 108
Archimédien
Théorème. [AuCA] p 12
L'ensemble des nombres réels vérifie la propriété d'Archimède, c'est à dire que pour tout nombre x réel et y réels positif non nul, on peut trouver un entier naturel n tel que x < ny soit :
On dit alors que IR est un corps archimédien car il vérifie cette propriété.
Histoire. [AuCA] p 12
Cette propriété porte le nom du célèbre mathématicien et physicien de l'antiquité ARCHIMEDE (287 - 212 av. J.-C.). Cependant, ARCHIMEDE l'attribue à EUDOXE de Cnide qui l'aurait énoncée un siècle auparavant.
La propriété est énoncée sous cette forme :
Il y a toujours un multiple du plus petit qui est supérieur au plus grand.Si l'on a 2 segments, on peut toujours, en multipliant le petit, dépasser le grand.
Arrangements. =>
Définition ([EscoJ] p 177)
Soit A un ensemble non vide. On appelle arrangement de p éléments de A toute p-liste (a1;...;ap) d'éléments deux à deux distincts.
Propriété : On note Anp le nombre d'arrangements de p éléments d'un ensemble de n éléments
et l'on a pour 0 ≤ p ≤ n, Anp = n! / (n - p)!
B.
Nombre de Bell (ou nombre exponentiel). =>
Définition. [HaSu]p27
Pour tout entier naturel n on appelle nombre de Bell ou nombre exponentiel le nombre de partitions d'un ensemble à n éléments.
Une partition d'un ensemble E est par définition un ensemble de parties non vides et disjointes deux à deux, dont la réunion est égale à l'ensemble E.
Ainsi si Bn désigne le nombre de partition d'un ensemble ayant n éléments on a :
B0 = 1 ; B1 = 1 ; B2 = 2 ; B3 = 5 ; B4 = 15 ; B5 = 52 ; B6 = 203 ;
et ils vérifient la relation :

C.
Calcul différentiel =>
- De nombreux développements dans la catégorie Analyse à plusieurs Variables.
Cardinal.
Définition.
Le cardinal d'un ensemble est le nombre d'éléments de cet ensemble. Pour le cas des ensemble infinis évidement il y a quelques problèmes ...
Histoire.
BOLZANO Bernard Placidus Johann Nepomuk (1781-1848) s'intéresse aussi avant CANTOR aux ensembles infinis. Il démontre que IR, le segment [0;1] et le segment [0;2] ont le même cardinal ce qui défie l'entendement à l'époque.
[HaSu]p45
Cholesky (factorisation de Cholesky ou décomposition de Cholesky).
Théorème. [MonAl2] p 214
Pour toute matrice H hermitienne et définie positive, il existe une matrice T, triangulaire supérieure et inversible telle que : H = T*.T
Remarques : [MonAl2] p 182, 208 , 210
1°) H hermitienne ssi H* = H et Hn l'ensemble des matrices hermitiennes est un IR-ev.
2°) H hermitienne positive ssi ( pour tout vecteur X on a : X*.H.X ≥ 0 ) ⇔ ( SpIR (H) ⊂ IR+ )
3°) H hermitienne définie positive ssi pour tout vecteur X on a : { X*.H.X ≥ 0 et (X*.H.X = 0 ⇒ X = 0 ) } ⇔ ( SpIR (H) ⊂ IR \ {0}+ )
Combinaisons. =>
Définition ([EscoJ] p 179).
Soit E un ensemble de cardinal n. On appelle combinaison de p éléments de E toute partie de E de cardinal p.
Propriété :
On note Cnp ou (pn ) le nombre d'arrangements de p éléments d'un ensemble de n éléments et l'on a pour 0 ≤ p ≤ n.
Pour tout n et p tels que 1 ≤ p ≤ n, 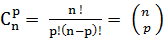
Conjecture de Bertrand (1822-1900), ou théorème de Tchebychev (1821-1894).
- Énoncé. [KoMe] p 101
Pour tout entier n > 2, il existe au moins un nombre premier compris entre les entiers n et 2n. - Histoire. [HaSu]p36
Cette conjecture est énoncée et admise par Joseph Bertrand. Il la vérifie jusqu'à 3 000 000.
Cependant elle n'est démontrée qu'en 1851 par Pafnouti Tchebychev ( 1821-1894) qui utilise dans sa démonstration l'inégalité qui porte son nom.
Le mathématicien hongrois Pavel Erdos (Budapest 1913) propose en 1932 une autre démonstration que l'on trouve sur le site anglais PlanetMath.
Le mathématicien allemand Robert Breusch (1960) l'améliore en 1931, il démontre que pour tout entier n > 47, il existe un nombre premier entre n et 9n/8.
Conjecture de GAUSS. (répartition des nombres premiers).
- Énoncé.
Le nombre de nombres premiers inférieurs à m tend vers m/ln m quand m tend vers l'infini. - Histoire. [HaSu]p300 et [Delah1] p 209
Pour tenter de démontrer (sans succès) cette conjecture, RIEMANN est amené à étudier les zéros de la fonction zêta.
Il émet alors l'hypothèse (hypothèse de RIEMANN) qu'ils ont tous une partie imaginaire égale à 1/2 (cette hypothèse est le 8ème problème de HILBERT (voir problèmes de HILBERT) et est toujours ouverte.
Cette conjecture est démontrée et devient le théorème des nombres premiers.
Conjecture de GOLDBACH.
Énoncé.
Tout nombre entier pair est la somme de deux nombres premiers.
Histoire. [HaSu]p148
Cette conjecture est présente ,sans démonstration, dans une lettre de 1742, du mathématicien russe GOLDBACH Christian (1690-1764) au mathématicien suisse EULER Leonhard (Bâle 1707 - Saint-Pétersbourg 1783).
Le mathématicien anglais WARING Edward (1734-1798) reprend cette affirmation en 1770 dans Meditationes algebraicae, en y ajoutant que tout nombre impair est la somme de troisnombres premiers. Ces problèmes demeurent encore non démontrés à ce jour (2007).
Constante d'Euler (ou constante gamma d'Euler).
Limite de la suite Un = 1 + 1/2 + 1/3 .... + 1/n - ln(n) est appelée constante d'Euler et notée γ (gamma)
Une valeur approchée de γ est 0,577 215 664 901 532.
On ne sait toujours pas en 2012 si ce nombre est rationnel ou irrationnel, algébrique ou transcendant.
Références : ( [AuCA] p 28 et [Gour1] p 206)
Continue, fonction.
Histoire.
En 1834, BOLZANO Bernard Placidus Johann Nepomuk (1781-1848) donne le premier exemple d'une fonction continue sur IR et dérivable en aucun point. Cependant cet exemple restera méconnu, si bien que WEIERSTRASS pense donner le premier exemple de ce type en 1861. [HaSu]p45
- Pour en savoir plus : La notion de Fonction.
Continu, Hypothèse du.
=> L'Hypothèse du continu et Georg CANTOR (1945 - 1918)
Convergence commutative. (Pour les séries).
Définition. [TisAgreg] p155
On dit qu'une série est commutativement convergente si toute permutation de IN conserve la nature et éventuellement la somme de la série.
Théorème : Toute série réelle absolument convergente est commutativement convergente et la réciproque est vraie pour les séries réelles. [TisAgreg] p155
Théorème : On peut permuter les termes d'une série numériques semi-convergente de telle façon que l'on obtienne une série convergent dont la somme est égale à un nombre réel quelconque donné à l'avance. [TisAgreg] p191
Convergence uniforme : Pour les suites et les séries. =>
Énoncé. [AuCA] p 264 et p266
- Pour les suites.
La suite de fonctions (Sn) converge uniformément sur une partie D de IK vers la fonction S si :
∀ ε > 0 ; ∃ N(ε) ∈ IN tel que ∀t ∈D ( n > N(ε) ⇒ | Sn(t) - S(t) | < ε )
ou encore si :
lim sup t ∈D | Sn(t) - S(t) | = 0 ou avec la norme sup : lim || Sn(t) - S(t) || ∞ = 0 - Pour les série,
La définition est la même en prenant Sn(t) la somme partielle : Sn(t) = u0(t) + ... + un(t),
Sn(t) - S(t) représente alors le reste de la série (au signe près).
On peut aussi utiliser le critère de CAUCHY uniforme : la suite (Sn) cv uniformément sur D ssi elle vérifie le critère de Cauchy uniforme soit : ∀ ε > 0 ; ∃ N(ε) ∈ IN tel que ∀n > N(ε) ∀p ∈ IN on a || Sn(t) - S(t) || ∞ < ε
Histoire. [Dieudo] p 254
En 1838, le mathématicien allemand GUDERMANN Christophe (1798-1852), le professeur de WEIERSTRASS Karl Theodor Wilhelm (1815-1897), publie un article dans le Journal de Crelledans lequel il utilise la notion et le mot de convergence uniforme (im ganzen gleichen Grad)....
Coordonnées barycentriques.
Théorème. [Ladeg] p 43
Un système de coefficient barycentriques homogène (a,b,c) d'un point M du plan affine P dans la base affine (A,B,C) de ce plan (i. e. : trois points non alignés) est formé des trois déterminants suivants, relatifs à une base vectorielle quelconque :
a = det | vect(MB) , vect(MC) | ; b = det | vect(MC) , vect(MA) | ; C = det | vect(MA) , vect(MB) | ;
Ils sont proportionnels aux aires algébriques des triangles orientés MBC, AMC, ABC.
Approche historique.
Le mathématicien allemand MOBIUS August Ferdinand (1790-1868) introduit (conjointement à PLUCKER et FEUERBACH) les coordonnées barycentriques. [HaSu] p242
Coordonnées plückeriennes.
Définition et théorème. [HaSu]p283
Un système de la forme : { cx - bz = u ; az - cx = v ; bx - ay = w } où au + bv + cw = 0 et où a, b et c ne sont pas tous nuls, détermine une droite de l'espace, et toute droite admet un tel système d'équations. Les scalaires a, b, c, u, v, w sont les coordonnées plückeriennes de la droite.
Coordonnées polaires
Approche historique.
BERNOULLI Jakob, francisé Jacques (Bâle 1657 - Bâle 1705) est le premier à introduire les coordonnées polaires et il sait dériver avec de telles coordonnées. [HaSu]p30
Corps
Définition. [Gour2] p 53
Soit IK un ensemble muni de 2 lois internes + et ×. ( IK ; + ; × ) est un corps si :
( IK ; + ) est un groupe commutatif (on dit aussi abélien).( IK \ {0} ; × ) est un groupe.La loi × est distributive par rapport à la loi +.
- Remarques :
Si de plus la loi × est commutative, on dit que le corps ( IK ; + ; × ) est commutatif.Un corps est un anneau dans lequel tout élément non nul est inversible.Par exemple ( Q ; + ; × ), ( IR ; + ; × ), ( C ; + ; × ), ( Z / pZ ; + ; × ) sont des corps, que l'on note souvent Q, IR, C, Z / pZ en omettant de préciser les deux lois + et ×.Soit IL ⊂ IK, on dit que ( IL ; + ; × ) est un sous corps de IK si la restriction à IL des lois de IK lui confère une structure de corps.
Approche historique.
C' est le mathématicien allemand DIRICHLET Gustav Peter Lejeune (1805-1859), dans le Xe supplément aux Leçons de Théorie des nombres (1871), qui introduit les notion de corps et demodule, dans le sens que nous donnons actuellement à un sous-corps et à un sous-Z-module. [Dieudo] p 110
En 1898, le mathématicien allemand WEBER Heinrich (1842-1913) donne ("enfin") au terme corps (commutatif) le même sens général qu'aujourd'hui et il considère alors que les "imaginaires de GALOIS" forment un corps fini. [Dieudo] p 110
Critère de CAUCHY uniforme. (Pour les suites et les séries)
Définition. [AuCA] p 264 et p266
La suite de fonctions (Sn) vérifie le critère de Cauchy uniforme sur D (de IK) si :
∀ ε > 0 ; ∃ N(ε) ∈ IN tel que ∀n > N(ε) ∀p ∈ IN on a || Sn(t) - S(t) || ∞ < ε
- Remarque :
Dans le cas ou les fonctions sont bornées, ce critère montre que l'espace vectoriel ( B (D;IK) ; ||. || ∞) est un espace vectoriel normé complet (toute suite de Cauchy converge) donc que c'est un espace de Banach.
Propriété : La suite (Sn) cv uniformément sur D ssi elle vérifie le critère de Cauchy uniforme.
Histoire. [Dieudo] p 255
Dans son mémoire de 1853, le français CAUCHY Augustin-Louis (1789-1857) introduisit pour la première fois une notion rigoureuse de convergence uniforme (mais il ne la qualifie pas d'uniforme). Il utilise pour cela ce que l'on appelle maintenant le critère de Cauchy uniforme.
C'est cependant le mathématicien allemand WEIERSTRASS Karl Theodor Wilhelm (1815-1897) qui le premier énoncera et démontrera les théorème d'intégrabilité et de continuité de la somme d'une série de fonction. Dans son cours inédit de 1861, il définit la convergence uniforme (Konvergenz in gleichen Grad) à l'aide du critère de Cauchy et démontre que si la série de fonctions continues converge uniformément sur [a;b], alors sa somme est une fonction continue dans [a;b]. Sa démonstration est très proche de celle que l'on propose aujourd'hui.
D.
Dérivable, fonction
Histoire.
En 1834, BOLZANO Bernard Placidus Johann Nepomuk (1781-1848) donne le premier exemple d'une fonction continue sur IR et dérivable en aucun point. Cependant cet exemple restera méconnu, si bien que WEIERSTRASS pense donner le premier exemple de ce type en 1861. [HaSu]p45
Dérivée
Approche historique.
Dans sa Méthodes des tangentes, Isaac Barrow (1630 - 1677) introduit le triangle différentiel qui préfigure une approche géométrique de la notion de dérivée. ([HaSu]p10)
Dérivées partielles.
Histoire ⇒ l'histoire des fonctions de plusieurs variables.
Cours et théorèmes ⇒ cours sur le calcul différentiel et les dérivées partielles.
Déterminant
Définition et théorème. [Gour2]p135
L'ensemble des n-formes linéaires alternées sur un IK-ev E de dimension n est un IK-ev de dimension 1. De plus il existe une et une seule forme n-linéaire alternée prenant la valeur 1 sur une base B donnée de E.
Cette forme s'appelle déterminant dans la base B et on la note det B
Propriété :
On a pour (x1, ..., xn) ∈ E , detB (x1, ..., xn) = ∑ ε(σ). x1,σ(1)..... xn,σ(n)
ou σ décrit le groupe des permutations de {1,..,n}, Sn.
![]()
De même le déterminant d'une matrice carrée A est celui de ses vecteurs colonnes.
Histoire.
Le français VANDERMONDE Alexandre Théophile (1735-1796), est le premier à étudier les déterminants pour eux-même, et non pas pour l'unique usage qu'on leur destine à l'époque, la résolution de systèmes. Il donne la règle de calcul par le développement des mineurs d'ordre 2 et leurs complémentaires (qui sera généralisée par LAPLACE). [Audi]
Le mathématicien français LAPLACE Pierre Simon, marquis de (1749-1827), propose une méthode de calcul d'un déterminant qui porte son nom. Ce développement de LAPLACE est la méthode classique de développement d'un déterminant selon une ligne ou une colonne. [HaSu] p207
Le mathématicien allemand WEIERSTRASS Karl Theodor Wilhelm (1815-1897), est le premier à définir le déterminant d'une matrice comme un polynôme homogène linéaire par rapport à chaque ligne et chaque colonne, qui change de signe lorsqu'on permute 2 colonnes et qui vaut 1 pour l'identité. [Audi] p 364
Divergence (opérateur)
⇒ Les opérateurs différentiels.
Droite de Simson d'un triangle.
Définition.
Dans un triangle ABC, soit M un point du plan et U, V et W les projetés orthogonaux de M sur les droites (BC), (AC) et (AB). Alors M est sur le cercle circonscrit au triangle si et seulement si U, V et W sont alignés.
Dans ce cas, la droite passant par les points U, V et W s'appelle la droite de Simson associée au point M.
En particulier, la droite de Simson de chacun des sommets est la hauteur issue du sommet. De plus, la droite de Simson du point diamétralement opposé à un sommet sur le cercle circonscrit est le côté opposé à ce sommet.
Histoire.
SIMSON Robert (1687 - 1768) est un mathématicien anglais.
Droite de Steiner
Définition. [HaSu]p326
La droite de Steiner d'un point M du cercle circonscrit au triangle ABC est la droite image de la droite de Simson de M par l'homothétie de centre M et de rapport 2. Elle passe par l'orthocentre du triangle et par les symétriques de M par rapport aux côtés du triangles.
Histoire.
Jakob STEINER né le 18 mars 1796 et mort le 1er avril 1863, est un mathématicien suisse.
E.
Équation différentielle d'Euler
Une équation différentielle d'Euler ou de Cauchy-Euler est une équation différentielle linéaire de la forme.
![]()
La plus commune des équations de Cauchy-Euler est l'équation du second ordre, apparaissant dans un certain nombre d'applications en physique.
Par exemple lors la résolution de l'équation de Laplace en coordonnées polaires on obtient :
![]()
Équipollence
Définition. [RaDeOd2] p125
La notion équipollence est peu employée de nos jours dans les cours de mathématiques.
Autrefois on définissait le vecteur comme un représentant de la classe d'équivalence pour une relation d'équipollence des bipoints.
Dans un espace affine, on dit que deux couples de points (A,B) et (C,D) sont équipollence, si les vecteurs AB et CD sont égaux.
Histoire. [HaSu] p27
C'est BELLAVITIS Giusto (1803-1880) qui développe la notion d'équipollence.
Espace vectoriel
Définition. [Gour2] p107
On appelle IK-espace vectoriel (ou e.v. sur IK) un ensemble E muni d'une loi interne (notée +) et d'une loi externe (notée .) admettant IK comme ensemble d'opérateurs et vérifiant :
(1) : (E;+) est un groupe abélien (c.a.d. commutatif)
(2) : Pour tout x et y de E, et a, b de IK
• (2a) : a.(x+y) = a.x + b.y
• (2b) : (a+b).x = a.x + b.x
• (2c) : a.(b.x) = (ab).x
• (2d) : 1.x = x
Espace de Banach
Définition. [Gour1] p47
Un IK-espace vectoriel normé est un espace dit de Banach s'il est complet.
Histoire.
BANACH Stefan (1892-1945), un des fondateur de l'analyse fonctionnelle introduit la notion d'espace vectoriel normé en 1920. Cette notion est à la même époque aussi définie par Riesz, Hahn, Helly et Wiener. [HaSu] p24
Espace de Complet
Définition.[AuCA] p47
Un IK-espace vectoriel normé E est dit complet, si toute suite de Cauchy de E est convergente dans E. On dit alors que E est un espace de Banach. (IK est un corps, IR ou C).
Espace de Hilbert. (ou hilbertien)
Définition. [MonAn2] p 94
On appelle espace de Hilbert tout espace préhilbertien complet (pour la norme associée au produit scalaire).
- Remarque : préhilbertien (e.v. muni d'un p.s.) et complet (toute suite de Cauchy y converge)
Propriétés.
1°) Tout espace préhilbertien de dimension finie est un espace de Hilbert, car tout evn de dimension finie est complet.
2°) Il existe des espaces préhilbertien non complet.
3°) l², l'ensemble des suite (un) telles que la série ∑|un|² converge, est un espace de Hilbert.
Histoire. [HaSu] p171, p314
HILBERT généralise au début du 20ème siècle la notion de produit scalaire à des espaces de suites. On doit cependant en 1927 à VON NEUMANN l'axiomatisation de ces espaces dits préhilbertiens et hilbertiens.
SCHMIDT Erhard (1876-1959) introduit la notion d'opérateur auto-adjoint dans les espaces de Hilbert.
Espace préhilbertien. (ou préhilbertien)
Définition. [MonAn2] p 88
On appelle espace préhilbertien réel (resp. complexe) tout couple (E ; φ) où E est un IR-ev (resp. C-ev) et φ un produit scalaire sur E.
Histoire. [HaSu] p171
HILBERT généralise au début du 20ème siècle la notion de produit scalaire à des espaces de suites. On doit cependant en 1927 à VON NEUMANN l'axiomatisation de ces espaces dits préhilbertiens et hilbertiens.
Espace vectoriel normé, espace métrique
Définition. [Gour1] p47
Un IK-espace vectoriel est dit normé s'il est muni d'une norme II.II. En notant d(x;y) = IIx-yII, on en fait un espace métrique.
Histoire.
BANACH Stefan (1892-1945), un des fondateur de l'analyse fonctionnelle introduit la notion d'espace vectoriel normé en 1920. Cette notion est à la même époque aussi définie par Riesz, Hahn, Helly et Wiener. [Dieudo] p24
Hilbert (1862 - 1943) est le premier à développer la théorie des espaces vectoriels normés de dimension infinie.
[Gour1] p7
Le mathématicien français FRÉCHET Maurice (1878-1973) travaille initialement sur l'analyse fonctionnelle et cela le pousse à trouver un cadre plus général que la métrique euclidienne.
Il introduit les espaces métriques et propose les premières notions de topologie. [HaSu] p 131
Espace topologique : voir topologie
Espérance
Définition. [EscoJ]p55 et 123
- Cas discret :
Soit X une variable aléatoire discrète. On appelle espérance de X le réel noté E(X) :
E(X) = ∑xi.P(X = xi) pour i de 1 à n. - Cas continu : Soit X une variable aléatoire de densité f. On appelle espérance de X le réel noté E(X) :
E(X) = ∫t . f(t) dt sur IR
Histoire. [HaSu] p179
C'est le mathématicien HUYGENS Christiaan (1629-1695) qui introduit cette notion.
Étoilé
Définition. [MonAn2] p 581
Soit U une partie de IRp. U est étoilé si il existe un point A de U tel que ∀M ∈ U ; [AM] ⊂ U.
On dit aussi que U est étoilée par rapport au point A.
On dit que U est étoilé si il existe A tel que U soit étoilée par rapport à A.
- Remarque : Toute partie convexe est étoilée par rapport à chacun de ses points.
Exacte (forme différentielle)
Définition. [MonAn2] p 581
Soit U un ouvert de IRp et w une forme différentielle sur U.
On dit aussi que w est exacte sur U (ou w admet des primitives sur U) si il existe F : U → IR de classe C1 sur U telle que :
Pour tout (x1, ..., xp) de U, d(x1, .. , xp) F = w(x1, .., xp)
- De nombreux développements dans la catégorie Analyse à plusieurs Variables.
Exponentielle. (e, le nombre e.) =>
Le nombre e est une constante mathématiquenote 1 valant environ 2,71828 et parfois appelée « nombre d'Euler » ou constante de Néper en référence aux mathématiciens Leonhard Euler et John Napier.
Ce nombre est défini à la fin du XVIIe siècle, dans une correspondance entre Leibniz et Christian Huygens, comme étant la base du logarithme naturel. Autrement dit, il est caractérisé par la relation
$$ln(e) = 1$$
ou de façon équivalente il est l'image de 1 par la fonction exponentielle, d'où la notation
$$exp(x) = e^x$$
La décomposition de cette fonction en série entière mène à la définition de e par Euler comme somme de la série :
$$\displaystyle \mathrm {e} =1+{\frac {1}{1}}+{\frac {1}{1\times 2}}+{\frac {1}{1\times 2\times 3}}+{\frac {1}{1\times 2\times 3\times 4}}+\cdots =\sum _{n=0}^{+\infty }{\dfrac {1}{n!}}$$
Ce nombre apparait aussi comme limite de la suite numérique de terme général (1 + 1/n)n et dans de nombreuses formules en analyse telles l'identité d'Euler
$$e^{i\pi}+ 1 = 0$$
ou la formule de Stirling qui donne un équivalent de la factorielle. Il intervient aussi en théorie des probabilités ou en combinatoire.
Le mathématicien français Jean Bernouilli (1667-1748) introduisit les fonctions exponentielles dans une correspondance avec le mathématicien allemand Gottfried Wilhelm Leibniz (1646-1716) en 1694.
Le mot «exponentielle» apparaît pour la première fois dans la réponse de Leibniz.
C'est en 1778 que le mathématicien suisse Leonhard Euler (1707-1783) utilisa pour la première fois la notation \(e\). Euler démontre que e est irrationnel, donc que son développement décimal n'est pas périodique, et en donne une première approximation avec 23 décimales. Il explicite pour cela son développement en fraction continue.
Le mathématicien français HERMITE Charles (1822-1901) doit sa notoriété à sa démonstration, en 1873, de la transcendance du nombre \(e\). Il démontre que \(e\) n'est racine d'aucune équation polynomiale à coefficients entiers. [HaSu] p167
- Pour des compléments : La fonction exponentielle et le nombre e / Oraux ENS
Exposant
Définition.
Un nombre réel a élevé à la puissance n (pour n entier non nul) est défini par an = a×a×a×...xa. (n fois).
Par exemple 3² = 3×3 = 9 et 23 = 2×2×2 = 8
Par convention on a a0 = 1 alors que 00 n'est pas défini.
On peut généraliser cette définition pour n réel et a > 0 à l'aide de la fonction exponentielle : an = en.ln a.
=> lien vers un document de cours de collège.
Histoire. Pour en savoir plus =>
Extremums :
- De nombreux développements dans la catégorie Analyse à plusieurs Variables.
F.
Fermée. (Forme différentielle)
Définition. [MonAn2] p 580
Soit U une partie de IRp, et w une forme différentielle sur U.
w est fermée sur U si pour tout i, j de {1,..,p}; ∂Ai/∂xj = ∂Aj/∂xi où Ai sont les coefficient de w.
FIBONACCI suite de
Définition.
La Suite de Fibonacci (Un) est définie, par récurrence, par Uo = U1 = 1 et, pour tout entier naturel n, Un+2 = Un+1 + Un.
Le quotient Un+1 / Un. converge vers le nombre d'or (1+V5)/2.
Histoire. [HaSu] p127
Cette suite est introduite en 1202 par FIBONACCI. Le problème posé est le suivant: Partant d'un couple, combien de couples de lapins obtiendrons-nous après un nombre donné de mois sachant que chaque couple produit chaque mois un nouveau couple, lequel ne devient productif qu'après deux mois.
Fonction f(.)
Histoire. [HaSu] p244
- Le mot fonction est emprunté sous la forme simplifié funcion (1370) au latin functio "accomplissement, exécution" , en français courant [Rey].
- Au 18ème Euler (1707-1783) propose l'idée qu'une suite de courbes, donc d'expressions, représentait une fonction. [EtcGarVer] page55.
- C'est Leibniz (1646-1716) qui utilise le mot fonction pour la première fois en mathématiques en 1673, mais la première définition fut donnée par J.Bernouilli (1654-1705). [HaSu] p213
- Pour le symbole f(.), il a été introduit par Euler en 1734 dans Commentarii Academiae Scientiarum Petropolitanae. [Cajo]
Voir histoire des symboles mathématiques =>
=> Pour des compléments, voir : Histoire de la notion de fonction.
Fonction Bêta. (fonction bêta d'EULER)
Définition. [MonAn2] p 226
La fonction Bêta est définie pour tout couple (x ; y) tel que x > 0 et y > 0 par :
![]()
Propriété : lien avec la fonction gamma. [MonAn2] p 226
On montre que : ∀(x,y) ∈] 0 ; + ∞[² :
![]()
Histoire. [HaSu] p39
Le célèbre mathématicien suisse, EULER Leonhard (Bâle 1707 - Saint-Pétersbourg 1783) étudie et introduit cette fonction. Dès 1729 il montre le lien entre la fonction gamma et la fonction Bêta. [Dieudo] p 36.
Le symbole de la fonction bêta d'EULER est introduit par le mathématicien et astronome français Jacques P. M. BINET (1786-1856) en 1839. (voir histoire des symboles mathématiques)
Fonction de Dirichlet.
Définition. [Dieudo] p 258
Une fonction classique non intégrable au sens de Riemann est la fonction qui dans [a;b], vaut 1 si x est rationnel, et 0 sinon.
Cette fonction est appelée, fonction de DIRICHLET.
Fonction Gamma ( ou fonction gamma d'Euler)
Définition. Cas réel. [AuCA] p 354 et p 359 ; [PreciAn2] p 323 ; [MonAn2] p 220 et p225
La fonction Γ est définie sur ]0 ; + ∞[ par : Γ(x) = ∫IR e-t . tx - 1 dt.
Elle fournit un prolongement de la factorielle car on démontre par une intégration par parties que :
Pour x dans ]0 ; + ∞[ : Γ(x + 1) = xΓ(x) et comme Γ(1) = 1 , on en déduit que pour tout n entier naturel Γ(n+1) = n!
Propriétés de la fonction Gamma.
Propriété 1 : Γ est de classe C∞ sur ]0 ; +∞ [ et est convexe. De plus : Γk(x) = ∫IR (lnt) k e-t t x - 1 dt.
Propriété 2 : Γ ' s'annule sur IR+ en un seul point c de ]1;2[ .
Propriété 3 : Γ(x) est équivalent à 1/x quand x tend vers 0+, soit Γ(x) ~ 1/x quand x → 0+.
Propriété 4 : Γ(x)/x → + ∞ quand x → +∞
Propriété 5 : Γ(1/2) = √ π
Cas complexe. [ServAn3 ] p 98
On peut aussi généraliser la définition de la fonction Gamma au plan complexe.
Pour tout z complexe, on définie : Γ(z) = ∫IR e-t . tz - 1 dt.
On montre alors que cette intégrale est définie et continue pour tout z tel que Re(z) >0.
Elle converge uniformément (absolument) sur toute partie du plan complexe vérifiant 0 < a ≤ Re(z) ≤ b < +∞.
Histoire.
Le célèbre mathématicien suisse, EULER Leonhard (Bâle 1707 - Saint-Pétersbourg 1783) étudie et introduit cette fonction. Dès 1729 il montre son lien avec la fonction Bêta.[Dieudo] p 36
Le symbole de cette autre fonction d'EULER est introduit par Adrien-Marie LEGENDRE (1752-1833) dans son Exercices de Calcul intégral sur divers ordres de transcendantes et sur les quadrantes. [Cajo] (voir histoire des symboles mathématiques)
Fonction indicatrice d'Euler (ou fonction d'Euler, notée phi).
Définition.[MonAl1] p 127, [KoMe] p42, [Calais] p 104
φ(n) ou Φ(n) selon les ouvrages, est le nombre d'entiers naturels non nuls, inférieurs à n et premiers avec n.
![]()
- Par exemple :
φ(6) = 2 car 6 est premier avec les deux entiers non nuls 4 et 5,
et φ(12) = 4.
On montre les propriétés suivantes de la fonction d'Euler.
- Propriété 1 : Si a est premier avec b (a^b = 1) alors φ(ab) = φ(a) × φ(b).
- Propriété 2 : Si p est alors pour tout nombre entier non nul r, φ(pk) = pk - pk-1
- Propriété 3 : Si n un entier non nul admet la décomposition primaire: n = ∏ piki, (pour i de 1 à q) alors

Histoire. [Cajo]
L'historien des sciences CAJORI Florian ( Suisse 1859 - Californie, USA 1930) indique que le symbole φ(m), pour désigner la fonction d'EULER, est introduit par Carl Friedrich GAUSS (1777-1855) en 1801 dans ses Disquisitiones arithmeticae.
Cette fonction fut étudiée initialement par EULER Leonhard (Bâle 1707- Saint-Pétersbourg 1783), qui ne la nomme pas ou la nomme πN dans ses travaux (pour plus de précisions voirhistoire des symboles).
Fonctions de plusieurs variables
Histoire ⇒ l'histoire des fonctions de plusieurs variables
Cours et théorèmes ⇒ cours sur le calcul différentiel et les dérivées partielles.
Fonction Zêta (ou dzêta) de Riemann : voir Zêta
Formes différentielles ⇒
- De nombreux développements dans la catégorie Analyse à plusieurs Variables.
Formule du crible ou de Poincaré
Définition.
Soient A1, ..., An , n ensembles finis. Nous avons
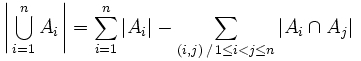
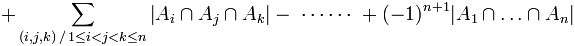
où |A| désigne le cardinal d'un ensemble fini A.
Cette formule peut aussi s'écrire de façon plus condensée
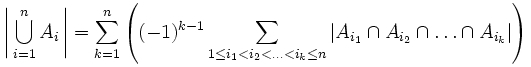
Version probabiliste

Par exemple on obtient :
- P(AUB) = P(A) + P(B) - P(A∩B)
- P(AUBUC) = P(A) + P(B) + P(C) - P(A∩B) - P(A∩C) - P(B∩C) + P(A∩B∩C)
- P(AUBUCUD) = P(A) + P(B) + P(C) + P(D) - P(A∩B) - P(A∩C) - P(A∩D) - P(B∩C) - P(B∩D) - P(C∩D) + P(A∩B∩C) + P(A∩B∩D) + P(A∩C∩D) + P(B∩C∩D) - P(A∩B∩C ∩D)
Histoire
En combinatoire, le principe d'inclusion-exclusion permet d'exprimer le nombre d'éléments (ou cardinal) d'une réunion finie d'ensembles finis en fonction du nombre d'éléments de ces ensembles et de leurs intersections.
Il se traduit directement en termes de probabilités.
Il est attribué au mathématicien Abraham de MOIVRE, et connu également (lui ou sa version probabiliste) sous le nom de formule du crible de Poincaré, formule de Poincaré, ou formule du crible.
Formule de Moivre
Définition.
(cos x + i sin x) n = cos nx + i sin nx ou en notation exponentielle, (eix)n = einx
Histoire. [HaSu] p244
On trouve cette formule dans les travaux de DE MOIVRE mais il semble que COTES la connaissait déjà.
Sa formulation actuelle et son extension à tout nombre réel n est due à EULER vers 1750.
Formule de Stirling
Théorème. [AuCA] p 339
- n! ≈ (n/e)n √(2πn) quand n tend vers l'infini soit :
![]() ou
ou
- limite quand n tend vers l'infini de n! / [ (n/e)n √(2πn) ] égale 1 soit :
![]()
Histoire. [HaSu] p244 et p 330 et [Dieudo] p 26
Cette formule est due en fait à DE MOIVRE Abraham (1667-1754) qui la démontre avec une constante, sans expliciter le terme √(2π).
Le mathématicine anglais STIRLING James (1692 - 1770) montre lui que la constante est √(2π).
STIRLING établit en 1730 un développement de ln n! avec cinq termes, l'équivalent de n! est donné la même année par DE MOIVRE Abraham (1667-1754).
Formules de Taylor
Histoire. [HaSu] p339
En 1755, le mathématicien anglais TAYLOR Brook (1685-1731) énonce la formule qui porte son nom, sans reste et sans se préoccuper des problèmes de convergence. Il l'utilise pour trouver des solutions approchée d'une équation f(x) = 0, en ne conservant que des termes inférieurs ou égaux à 2.
G.
Gamma, Constante d'Euler
- Voir Constante d'Euler.
Gamma, fonction gamma
- Voir fonction gamma
Gradient (opérateur)
GRAM (déterminant de Gram et matrice de Gram)
Définition. [Gour2] p 259
Soit E un espace préhilbertien (réel ou complexe) et x1,..,xn n vecteurs de E.
On appelle matrice de GRAM de x1, ..., xn la matrice ( φ( xi ; xj ) ) où φ un produit scalaire.
Le déterminant de Gram, est celui de la matrice de GRAM, on le note G(x1, ... , xn)
Propriété.
1°) Toute matrice de gram est hermitienne positive et réciproquement.
2°) Soit V un sous-espace de E muni d'une base (e1,..,en) (pas forcement orthonormale).
Soit x un vecteur de E, alors la distance d de x à V vérifie : d² = G(e1, .., en, x) / G(e1,..,en).
Histoire. [HaSu] p150
Le déterminant de Gram, est introduit par le mathématicien danois GRAM Jorgen Pedersen (1850-1916).
Groupe
Définition.
Un groupe est un ensemble muni d'une loi de composition interne (lci) :
- associative,
- admettant un élément neutre,
- et, pour chaque élément de l'ensemble, un élément symétrique.
Groupe quotient
Histoire.
JORDAN Camille Marie Ennemond (1838-1922), mathématicien français est le premier à prolonger la théorie de Galois et cela l'amène à définir la notion de groupe quotient. En 1872, il utilise pour la première fois la notation G/H pour désigner le quotient du groupe G par son sous-groupe H. [HaSu] p185
Gudermanien
Définition. [HaSu] p153
Gd(x), appelé gudermannien est unique élément de l'intervalle ]-π/2;π/2[ tel que tan Gd(x) = sh x.
Histoire.
GUDERMANN Christophe (1798-1852) est surtout connu pour avoir été le professeur du célèbre Karl WEIERSTRASS (1815-1897) alors que ce dernier préparait le professorat du second degré.
H.
HARDY notation <<
- Voir notation de Landau et Hardy.
Hermitienne (matrice hermitienne)
Définitions : [MonAl2] p 182, 208 , 210
Soit H une matrice carrée complexe de Mn(C)
1°) H hermitienne ssi H* = tconj(A) = H
2°) Hn, l'ensemble des matrices hermitiennes est un IR-ev.
3°) H hermitienne positive ssi ( pour tout vecteur X on a : X*.H.X ≥ 0 ) ⇔ ( SpIR (H) ⊂ IR+ )
4°) H hermitienne définie positive ssi pour tout vecteur X on a :
{ X*.H.X ≥ 0 et (X*.H.X = 0 ⇒ X = 0 ) } ⇔ ( SpIR (H) ⊂ IR \ {0}+ )
Holomorphe (fonction holomorphe)
Histoire. [HaSu] p 51
Les mathématiciens français BOUQUET Jean-Claude (1819-1885) et BRIOT Charles (1817 - 1882) introduisent les termes de fonction holomorphe et fonction méromorphe. [HaSu] p51
Horner (schéma de Horner)
Définition. [MonAl1] p 145
On remarque par exemple que a3.x3 + a2.x² + a1.x + a0 = a0 + (a1 + (a2 + a3.x).x).x
On part donc de b3 = a3 puis pour n de (3 - 1) à 0 : bn = an + bn-1.x , on a alors P(x) = b0.
- Par exemple si P(x) = 2x3 - x² + 3x + 4 = 4 + (3 + (-1 + 2x).x).x et donc pour calculer P(5) on calcule :
-
- b3 = a3 = 2
- b2 = a2 + b3.x = -1+ 2×5 = 9
- b1 = a1 + b2.x = 3 + 9×5 = 48
- b0 = a0 + b1.x = 4 + 48×5 = 244.
- On vérifie que P(5) = b0 = 244
-
Pour d'autres exemples, consultez le papier de Maoulida Ali Daoudou.
Histoire. [HaSu] p177 et p293
HORNER William George (1787 - Bath 1837) reste célèbre pour sa méthode de calcul des valeurs approchées des racines d'une équation numérique (le schéma de Horner). Cet algorithme serait en fait déjà connu des chinois, notamment de QIN JIU ZHAO (env. 1200 - env. 1260).
Hypothèse du continu
=> L'Hypothèse du continu et Georg CANTOR (1945 - 1918)
I.
Identités d'Euler
exp(ix ) = e ix = cos x + i sin x
et donc
-
- cos x = ( e ix + e -ix )/ 2
- sin x = (e ix - e -ix )/ 2i
- cos x = ( e ix + e -ix )/ 2
Inégalité de Bernoulli (Jacques)
Inégalité de Bernoulli Jacques.
Pour tout réel x > -1 et tout nombre entier n >1 : ( 1 + x)n > 1 + nx
Histoire.
BERNOULLI Jakob, francisé Jacques (Bâle 1657 - Bâle 1705) démontre en 1689 cette inégalité, que l'on retrouve cependant dès 1670 chez Barrow Isaac (1630 - 1677).
Inégalité de Cauchy-Schwarz
Inégalité de Cauchy-Schwarz. (CAUCHY Augustin-Louis (1789-1857) et SCHWARZ Hermann Amandus (1843-1921))
Soit (E, φ) un espace préhilbertien, pour tout (x;y) de E² ; on a :
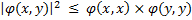
Que l'on peut aussi écrire :
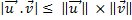
Avec égalité ssi les deux vecteurs sont liés (ou colinéaires)
Histoire. [Dieudo] p 341
Lors de la résolution de l'équation aux cordes vibrantes, le mathématiciens allemand SCHWARZ Hermann Amandus (1843-1921) utilise l'inégalité dite de SCHWARZ pour un produit scalaire dans un espace fonctionnel :
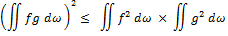
Cette inégalité est en fait introduite en 1859 par le mathématicien BUNIAKOWSKI mais sans démonstration.
Inégalité de Minkowski de MINKOWSKI Hermann (1864-1909)
Inégalité de Minkowski. [MonAn2] p 92 [Ladeg]p92
Soit (E, φ) un espace préhilbertien, Φ la forme quadratique associé au produit scalaire φ; on a :
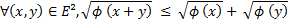
Que l'on peut écrire aussi :
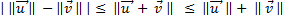
Cas d'égalité : [Ladeg]p92
- ssi l'un des deux vecteurs est nul ou si ils sont colinéaires de sens opposé.
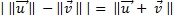
- ssi l'un des deux vecteurs est nul ou si ils sont colinéaires de même sens.
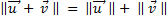
Histoire.
MINKOWSKI Hermann (1864-1909) est un mathématicien russe.
Intégrale, calcul intégral
Histoire.
En 1691, BERNOULLI Jakob, francisé Jacques (Bâle 1657 - Bâle 1705) introduit le terme calcul intégral dans son sens mathématique actuel. [HaSu] p30
J.
Jacobien (et matrice Jacobienne)
Définition. [AuCA] p 522
Soit f un fonction de IRp dans IRq, différentiable en un point a.
La matrice jacobienne de f en a est la matrice notée Jf(a) définie par Jf(a) = Mat ( ∂fi / ∂xj ) pour i de 1 à q et j de 1 à p.
Le jacobien de f en a sera le déterminant de cette matrice.
Histoire. [HaSu] p179
La matrice jacobienne et le jacobien furent introduits en 1929 par JACOBI Carl Gustav Jacob (1804-1851) et dénommés ainsi par SYLVESTER( 1814 - 1897). [HaSu] p184
L.
Lemme de Riemann - Lebesgue. =>
Lemme. [AuCA] p 429 et p 427
Soit f une fonction continue par morceaux sur un segment [a;b]. Alors :
lim ∫[a;b] f(t).e itx dt = 0 (quand x → + ∞) et lim ∫[a;b] f(t).e itx dt = 0 (quand x → - ∞)
=> Pour en savoir plus : Le théorème de Riemann
Loi de Poisson
Définition. [EscoJ] p 83 et [DegHEC] p 142
Soit λ > 0. La v.a.r X suit la loi de Poisson de paramètre λ si :
1°) X(Ω) = IN et 2°) Pour tout entier k, P( X = k) = e - λ λ k / k!
Propriétés. [DegHEC] p 142 et p 241
1°) On montre que E(X) = λ et V(X) = λ.
2°) Si (X1) est une suite de var indépendantes de loi P(λi), alors ∑ Xi suit la loi P(∑λi)
3°) Théorème : Soit λ ∈[0;1] et n entier n > 0. soit (Xn) une suite de var de loi binomiale B(n ; λ/n )
Alors (Xn) converge en loi vers une var de loi de Poisson P(λ).
En pratique, B(n;p) peut être approchée par la loi P(np) quand { p ≤ 0,1 ; n ≥ 30 ; np < 15 }
Histoire. [HaSu] p285
POISSON Denis Siméon (1781-1840) publie, en 1837, un traité sur les probabilités dans lequel on trouve pour la première fois la loi qui porte son nom, qu'il obtient comme limite de la loi binomiale B(n;p) avec np constant.
M.
Matrices.⇒
Méromorphe (fonction méromorphe)
Histoire. [HaSu] p 51
Les mathématiciens français BOUQUET Jean-Claude (1819-1885) et BRIOT Charles (1817 - 1882) introduisent les termes de fonction holomorphe et fonction méromorphe. [HaSu] p51
Module d'un complexe (Pour les propriétés des complexes)
Définition. [HaSu]p15
Le module d'un nombre complexe de la forme a+ib est |a+ib| = a² + b².
Le terme est du à Argand (1768 - 1822).
Propriétés. [MonAn1] p 69 (Pour les complexes z et z')
- |z . z'| = |z|.|z' |
- |z + z' | ≤ |z| + |z' | (Inégalité triangulaire)
avec égalité si z=0 ou si z' = kz (k réel positif) - |z|² = z. conj(z)
- | |z| - | z' | | ≤ |z - z' |
N.
Nabla (opérateur).
Nombres premiers.
Norme de SCHUR
Définition et Théorème . [SoroAlg] p347 et p349
L'application NS : Mn(IK) → IR qui à A → √tr(A*.A) est une norme sur Mn(IK) appelée norme de Schur.
Propriété.
Pour n >1, cette norme n'est pas subordonnée sur Mn(IK), c'est à dire qu'elle ne dérive pas d'un produit scalaire
car NS (In) = √n. Et √n ≠1 pour n > 1.
Or toute norme subordonnée sur Mn(IK) vérifie NS (In) = 1. (voir sa définition)
Norme subordonnée
Définition. [SoroAlg] p338
Soit ||.|| une norme sur IKn identifié à Mn,1 (IK). (IK est IR ou C).
1°) L'application N: Mn(IK) → IR qui à A → sup ||Ax|| pour ||x|| ≤ 1, est une norme sur Mn(IK) appelée norme subordonnée à ||.||.
2°) On la note souvent |||.|||.
3°) On a : ∀A ∈Mn(IK), N(A) = sup ||Ax|| pour ||x|| = 1
4°) On a : ∀A ∈Mn(IK), N(A) = sup ||Ax|| / ||x|| pour ||x|| ≠0
5°) N(In) = 1.
Notations de LANDAU o et de HARDY <<
Définition. [AuCA] p 77, [MonAn1] p 274
- Pour les suites :
Si (Un) est une suite, on écrit Un = o(1) pour traduire que lim Un = 0 (quand n → + ∞).
La notation Un = Vn o(1) signifie que la suite (Un) est négligeable par rapport à la suite (Vn),
Ce que l'on note aussi Un = o(Vn) ou Un<<Vn (notation de HARDY) - Pour les fonctions :
- Si f est une fonction définie sur une partie D de IR et si a ∈ adh(IR) = IRU{ + ∞, - ∞ },
on écrit f(x) = o(1) si n → a (on dit aussi "en a" ou "au voisinage de a") pour traduire que lim f(x) = 0 (quand n → a). - Si f et g sont des fonctions définies sur une partie D de IR et si a ∈adh(IR) = IRU{ + ∞, - ∞ },
La notation f(x) =a g(x) o(1) signifie que la fonction f est négligeable par rapport à la fonction g,
Ce que l'on note aussi f(x) =a o( g(x) ) ou f(x) << g(x) (notation de HARDY)
- Si f est une fonction définie sur une partie D de IR et si a ∈ adh(IR) = IRU{ + ∞, - ∞ },
Histoire. [HaSu] p 206
Le mathématicien allemand LANDAU Edmund Georg Hermann (1877-1938) introduit cette notation dans ses travaux. "Elle désigne une quantité variable qui tend vers 0".
Pour ce qui est de la première utilisation de ce symbole, les avis des spécialistes divergent.
O
Ombral (calcul)
Le calcul ombral ou théorie des opérateur linéaire permet de passer de formules à d'autres en utilisant des formes linéaires.
Il fut utilisé pour la première fois par le mathématicien BLISSARD John (1803, Northampton, England – 1875) et l'américain né en Italie, Gian-Carlo ROTA (USA, 1932-1999).
Le calcul symbolique est appelé parfois calcul ombral.
Utilisé sans grande rigueur depuis le début du 20 eme siècle, le calcul symbolique a été développé par John Blissard vers 1860 mais c'est E.T. Bell qui en donne des fondations rigoureuses près d'un siècle plus tard. (=> voir le texte)
Le mathématicien américain né en Italie, Gian-Carlo ROTA (USA, 1932-1999) est cependant considéré comme le fondateur de cette théorie qu'il développe en 1970.
P.
Partition.
Une partition d'un ensemble E est par définition un ensemble de parties non vides et disjointes deux à deux, dont la réunion est égale à l'ensemble E.
Chaque partie d'une partition de l'ensemble vide est une partie de l'ensemble vide donc est vide (cela est évident), et leur réunion est égale à l'ensemble vide. Donc, le singleton ensemble vide est la seule partition de l'ensemble vide.
Pour tout entier naturel n on appelle nombre de Bell ou nombre exponentiel le nombre de partitions d'un ensemble à n éléments.
Plan d'Argand-Cauchy.
Définition. [HaSu] p 15
Le plan d'Argant-Cauchy est la représentation géométrique des nombres complexes par un plan euclidien. Le nombre complexe a+ib étant identifié au point de coordonnées (a;b) dans un repère orthonormal du plan.
Histoire : Pour en savoir plus =>
Polynômes orthogonaux.
Définition. [ElJai] p102 et 108
Ces polynômes sont en fait une suite de polynômes qui peuvent selon le cas prendre le nom de polynôme de LEGENDRE, TCHEBICHEV, JACOBI, LAGUERRE, LAGUERRE généralisée, HERMITE.
- Voir l'article sur les Polynômes Orthogonaux =>
Probabilités.
- Voir l'article sur la naissance de la notion de Probabilité.=>
Problème du cavalier. (ou cavalier d'Euler).
Définition.
Le problème, ou encore algorithme du cavalier est un problème mathématico-logique.
Il consiste à établir les différentes façons de déplacer un cavalier sur un jeu d'échec (déplacement dit en L, deux cases en avant ou arrière, et une sur le côté). Ce cavalier doit visiter toutes les 8×8= 64 cases de l'échiquier, une seule fois, quelle que soit sa case de départ. Il s'agit alors de trouver l'ordre des 63 "sauts" du cavalier qui permettent, à partir d'une case donnée de trouver ce chemin.
Le problème du cavalier est connu depuis fort longtemps. Vers 840, al-Adli ar-Rumi en donne déjà une solution. On en trouve la première trace dans un traité indien, le Kavyalankara du poète Rudrata.
Le mathématicien Leonhard Euler est cependant le premier à l'avoir étudié scientifiquement en 1759. La « Solution d'une question curieuse qui ne paraît soumise à aucune analyse », n'est pourtant publié qu'en 1766.
A cette époque, l'académie des sciences de Berlin avait jugé le problème important et proposé une récompense pour le meilleur mémoire sur le sujet.
Parmi les milliards de solutions, seules 122 000 000 se terminent à un pas de la case de départ.
Le problème du cavalier est un cas particulier des graphes dits hamiltoniens. Il est relié à un champ extrêmement important et fécond des mathématiques appelé "théorie de graphes". Théorie récemment développée (elle est enseignée en terminale ES depuis 2001).
En 1997, un chercheur australien, Brendan McKay, conclut à l'existence de 13 267 364 410 532 circuits fermés (qui reviennent à la case de départ), plus de treize mille milliards de solutions.
Par contre, concernant les circuits ouverts, le problème l'est aussi (ouvert) !
On ne sait pas encore combien il y en a exactement. Récemment, Ernesto Mordecki, un mathématicien uruguayen, a prouvé en 2001 que le nombre de solutions au problème du cavalier dans sa forme général était inférieur à 1,3.1035 parcours (voir son exposé).
Problème de DIRICHLET (pour un disque).
Définition. [HaSu] p 104
Une fonction continue étant donnée sur le cercle de centre O , de rayon r dans le corps des complexes,
prolonger f en une fonction continue sur le disque fermé et harmonique sur le disque ouvert.
Histoire. [HaSu] p317
Le mathématicien allemand SCHWARZ Hermann Amandus (1843-1921) donne en 1870, la première démonstration d'existence du problème de DIRICHLET en dimension 2.
Q.
⇒ Quadratique (forme quadratique)
- Voir le développement =>
Quadrilatère de Lambert
Définition. [HaSu]p205
Le quadrilatère de Lambert est un quadrilatère ayant trois angles droits et le quatrième obtus.
R.
Règle de d'Alembert, (ou règle de d'Alembert-Gauss).
Énoncé. [AuCA] p 370
(Un) étant une suite de complexes (ou réels) non nuls à partir d'un certain rang.
On note L = lim sup | Un+1/Un| et l = lim inf | Un+1/Un|
- Si L < 1, la série ∑Un converge absolument,
- Si l >1 la série ∑Un diverge.
- Dans les autres cas il y a indécision.
Rotationnel (opérateur).
S.
SARRUS règle de (pour le calcul d'un déterminant).
Énoncé. [MonAl1] p 327
La règle de SARRUS (1798 - 1861) permet de calculer facilement un déterminant 3×3 (ou 2×2) et seulement ceux-ci.
Pour déterminer le déterminant de la matrice A = 
On reproduit les lignes de la matrice en dessous et on applique la règle suivante :


et
Det (A ) = somme des 3 diagonales descendantes - somme des 3 diagonales montantes :
Det (A) = a11×a22×a33 + a21×a32×a13 + a31×a12×a23 - a31×a22×a13 - a11×a32×a23 - a21×a12×a33.
Histoire.
Le mathématicien français SARRUS Pierre Frédéric (Saint-Affrique 1798 - 1861) publie cette règle dans son article, Nouvelles méthodes pour la résolution des équations en 1833.
Séries
Histoire.
BERNOULLI Jakob, francisé Jacques (Bâle 1657 - Bâle 1705) démontre avec rigueur la convergence de la série Σ1/n². [HaSu] p30
Séries de Bertrand (1822-1900)
Énoncé. [AuCA]p369
On appelle série de Bertrand celles de la forme ∑ 1 / [ na (ln n)b ].
Elles convergent pour a > 1 ou pour a = 1 et b > 1 et diverges dans les autres cas.
Séries harmonique
Définition. [AuCA] p 364
La série harmonique est la série définie par Hn = ∑ 1/k pour k de 1 à n.
Histoire. [HaSu] p266,p46
Le mathématicien français ORESME Nicolas (Oresme, près de Bayeux 1325 - Lisieux 1382) est le premier à "prouver" la divergence de la série harmonique par groupement de termes en utilisant en fait la négation du critère de Cauchy.
Avec les notations actuelles, on montre facilement que |H2n - Hn| ≥ 1/2 et donc que la suite Hn n'est pas une suite de Cauchy (donc elle ne peut converger car toute suite convergente est de Cauchy).
Surface
Histoire. [DaDaPe] p 137
L'étude de la forme de la Terre participe à l'évolution de l'étude générale des surfaces. Ainsi la représentation des surface plongées dans l'espace par des équations F(x,y,z) = 0 est développée.
Le mathématicien français CLAIRAUT Alexis-Claude (1713-1765) établit les équations de quelques surfaces quadriques (sphère, cylindre, paraboloïde, hyperboloïde à deux nappes, ellipsoïde). Puis le suisse EULER Leonhard (Bâle 1707 - Saint-Pétersbourg 1783) étudie l'équation générale du second degré en trois variables (celle qui représente les quadriques).
CLAIRAUT montre que les courbes gauches (courbes de l'espace) peuvent se décrire comme intersection de deux surfaces.
T.
Théorème de d'Alembert-Gauss, (ou théorème fondamental de l'Algèbre).
Énoncé.
Dans les corps C : Tout polynôme à coefficients complexes se factorise en un produit de polynômes du premier degré.
Ou pour être plus savant, le corps des complexes C est algébriquement clos.
Dans le corps IR : Tout polynôme à coefficient réels se factorise en un produit de polynômes à coefficients réels de degré 1 ou 2.
Approche historique. ([HaSu]p10, p147, p 141)
Le mathématicien hollandais GIRARD Albert (1595-1632), poursuivant les travaux de CARDAN, affirme : qu'un polynôme de degré n admet exactement n racines (comptés avec leur ordre de multiplicité).
Ce théorème appelé, encore aujourd'hui, théorème fondamentale de l'algèbre voit sa première démonstration proposée par D'Alembert (1717 - 1783). Cependant celle-ci est incomplète puisqu'elle considère connu le résultat suivant :
Soit P un polynôme à coefficients complexes, si z0 est un complexe tel que P(z0) ≠ 0, alors dans tout voisinage de z0 il existe un nombre z tel que |P(z)| < |P(z0)|.
En 1799, le mathématicien allemand GAUSS Carl Friedrich (1777-1855), passe sa thèse dont le sujet est la démonstration du théorème fondamentale de l'algèbre (appelé maintenantthéorème de d'Alembert-Gauss). Il remarque que les démonstrations de d'ALEMBERT, EULER et LAGRANGE sont incomplètes. Pour sa 1ère démonstration de 1799, il introduit la représentation plane des nombres complexes et raisonne géométriquement. GAUSS publiera 2 nouvelles démonstrations en 1816 et 1850.
Ce théorème est démontré complètement pour la première fois en 1806 par Argand (1768 - 1822)
Théorème de Baire.
Énoncé. [AuCA] p 245
Un espace topologique est dit de Baire (du nom du mathématicien René Baire) si toute intersection dénombrable d'ouverts denses est dense. De façon équivalente, un espace topologique est de Baire si une union dénombrable de fermés d'intérieur vide est d'intérieur vide.
Approche historique. ([HaSu]p22 et 266)
Le mathématicien américain OSGOOD William Fogg (1864-1943) démontre ce théorème en 1898, indépendamment de BAIRE qui le démontre en 1899.
Théorème de Bernoulli (Jacques).
Théorème de Bernoulli (Jacques 1654 - 1705). [EscoJ] p161
On considère des variables de Bernoulli indépendantes associées à la répétition de la même expérience aléatoire (pour laquelle on s'intéresse à un événement, appelé succès, noté S).
Xn = 0 si à la nième épreuve, on n'a pas S, et Xn =1 si à la nième épreuve, on a S.
En notant p = P(S), on a pour tout entier n non nul, Xn suit la loi B(p) et :
( X1 + X2 + ... + Xn)/n tend vers p en probabilité quand n tend vers l'infini.
Histoire.
BERNOULLI Jakob, francisé Jacques (Bâle 1657 - Bâle 1705) démontre avec rigueur la loi faible des grands nombres pour le jeu de pile ou face, appelé théorème de Bernoulli. [HaSu] p30
Théorème de Brun (1885 - 1978).
- Voir le développement =>
Théorème de Dini. =>
Sous certaines conditions, la convergence simple peut aussi entrainer la convergence uniforme, c'est ce que l'on nomme le théorème de DINI.
- Théorème de DINI, du nom du mathématicien italien Ulisse DINI (1845 - 1918). [Gour1]p229 et [Hauch2]
- Soit (fn) une suite croissante de fonctions réelles continues et définies sur un segment [a ; b] de IR.
Si (fn) converge simplement vers une fonction f continue sur [a;b], alors la convergence uniforme. - Soit (fn) une suite de fonctions croissantes réelles, continues et définies sur un segment [a ; b] de IR.
Si (fn) converge simplement vers une fonction f continue sur [a;b], alors la convergence uniforme.
- Soit (fn) une suite croissante de fonctions réelles continues et définies sur un segment [a ; b] de IR.
Le théorème fondamentale de l'Arithmétique.
- Voir le développement =>
Théorème de Fubini.
Théorème. [AuCA] p 568
Soit D un compact élémentaire et f une fonction continue sur D alors :
![]()
![]()
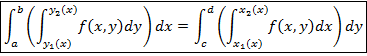
Approche historique. [HaSu]p135
Le mathématicien italien FUBINI Guido (1879-1943) reste célèbre pour avoir démontré en 1907 un théorème qui porte son nom et qui permet de ramener le calcul d'une intégrale de surface à celui de eux intégrales simples.
Théorème de Gauss - Wantzel.
Théorème. [HaSu] p362
En 1837, Pierre Wantzel (1841 - 1848) caractérise les nombre premiers constructibles.
Un nombre réel est constructible (à la règle et au compas) si il est racine d'un polynôme à coefficients entiers dont le degré est une puissance de 2.
On en déduit par exemple que la racine cubique de 2 n'est pas constructible, que la duplication du cube (construire l'arête d'un cube ayant un volume double de celui d'un cube donné) est impossible et que la trissection de l'angle est impossible.
Histoire.
En 1837, encore élève ingénieur, le mathématicien français Pierre WANTZEL publie dans le Journal des mathématiques pures et appliquées un article intitulé Recherches sur les moyens de reconnaître si un problème peut se résoudre avec la règle et le compas.
Il y expose un critère de non-constructibilité à la règle et au compas appelé théorème de Wantzel, et termine la démonstration initiée par Gauss sur les polygones constructibles (théorème de Gauss-Wantzel).
Théorème de Heine.
Théorème. [AuCA] p229, [Gour1] p 31
Soit E et F des espaces vectoriels normés (sur IR ou C), ou même deux espaces métriques,
et f une fonction continue d'un compact K de E sur F.
Alors f est uniformément continue
Histoire. [HaSu] p 164
Le mathématicien allemand Eduard Heine démontrer ce théorème en 1872, pour une fonction continue sur un segment [a;b] de IR.
Théorème de Mordell.
Théorème. [HaSu] p 247
Si k est un entier relatif non nul, l'équation de Mordell y² = x3 + k n'a qu'un nombre fini de solutions (x;y) où x et y sont des entiers relatifs.
Histoire. [HaSu] p 247
Le mathématicien anglais MORDELL Louis Joel (1888-1972) démontre ce théorème qui sera amélioré par Alan BAKER (Londres 1939) en 1967 sous la forme : Max { |x| ; |y| } ≤ e 10 ^10 . |k| 10 000
Théorème des Nombres premiers
- Voir développement =>
Théorème de Plancheret
Théorème. [HaSu] p281
Soit f une fonction intégrable et de carré intégrable sur IR, alors sa transformée de Fourier est de carré intégrable sur IR et ∫| f |² = ∫| tf(f ) |²
Théorème de Poincarré
Théorème. [MonAn2] p582
Soient U un ouvert de IRp et w une forme différentielle sur U.
Si U est étoilé et si w est fermée sur U, alors w est exacte (admet des primitives) sur U.
- Remarque 1 : U étoilé si il existe un point A de U tel que ∀M ∈ U ; [AM] ⊂ U.
- Remarque 2 : w fermée sur U si pour tout i, j ; ∂Ai/∂xj = ∂Aj/∂xi où Ai sont les coefficient de w.
- Pour des complément, voir la page : ⇒ Formes différentielles.
Histoire.
POINCARÉ Jules Henri (1854-1912) est un mathématicien français.
Théorème des quatre couleurs
Théorème.
Le théorème des quatre couleurs énonce la possibilité de colorier (on dit aussi colorer en théorie des graphes) avec quatre couleurs seulement une carte géographique sans que deux pays voisins aient la même couleur.
Théorème de raréfaction d'Euler (1707-1783)
- Développement =>
Théorème de raréfaction de Legendre(1752-1833)
Théorème de SCWHARZ.
Théorème de SCHWARZ. [MonAn2]p559
Soient U un ouvert de IRp, f une application de U dans IRp, a ∈U et 1 ≤ i , j ≤ p alors :
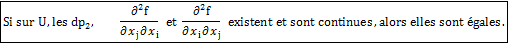
Histoire. [Encyclopédia Universalis] et [Dieudo] p 273
Dans le chapitre sur les fonctions de plusieurs variables de son cours de 1861, le mathématicien allemand WEIERSTRASS Karl (1815-1897) démontre que si f est continue, aisi que ses dérivées partielles premières et secondes alors on a l'égalité :
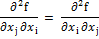
Ce théorème est ensuite généralisé par le mathématicien allemand SCHWARZ Hermann Amandus (1843-1921) en 1873.
Il montre que cette formule est valable si est valable si l'un des deux membres seulement est continu par rapport à l'ensemble des variables.
Le mathématicien italien PEANO Giuseppe (1858-1932) donne l'exemple de la fonction définie par :
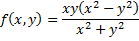
prolongée par continuité en posant f(0,0)= 0, pour laquelle les permutations des dérivées partielles n'est pas licite.
Théorème et formule de Stokes
Théorème. [VautAlg2] p 214
∫ϒ wV = ∫∫∑ dwV
Formules de Stokes. [VautAlg2] p 213
Soit K un k-compact régulier d'un élément de k-surface S de l'espace vectoriel E de dim p ≥ k.
Soit w une (k-1)-forme différentielle de classe C1 sur S.
Alors ∫∂K w = ∫K dw
- Par exemple si k = 3, w = x.dy∧dz + y.dz∧dx + z.dx∧dy.
Le bord du tétraèdre K=OABC de IR3 est la réunion des 4 faces orientées vers l'extérieur.
Comme w s'annule sur les 3 faces contenant 0,
on a : ∫∂K w = ∫(ABC) w = ∫K dw = 3 ∫∫∫K dx∧dy∧dz = 3 fois le volume du tétraèdre (OABC)
Théorème des Valeurs Intermédiaires. (ou TVI)
Théorème des valeurs intermédiaires (ou T.V.I). [AuCA] p102
Soit f une fonction continue sur le segment [a;b].
Si f(a) et f(b) sont de signe contraires, alors f s'annule au moins une fois sur l'intervalle ]a;b[.
Histoire.
Dans son premier ouvrage Rein analytischer Beweis... BOLZANO Bernard (1781-1848) démontre le théorème des valeurs intermédiaires sans utiliser l'évidence géométrique comme on le faisait alors.
Le titre de l'ouvrage Rein analytischer Beweis..(1817) est l'énoncé complet du théorème des valeurs intermédiaires. [HaSu] p45
Théorème de WEDDERBURN.
Théorème de WEDDERBURN. [Gour2] p 94
Tout corps fini est commutatif.
Histoire. [Gour2] p 94 et [HaSu] p364
La démonstration de ce théorème fut donné indépendamment par les mathématiciens américains WEDDERBURN Joseph Henry Maclagan (1882-1948) et DICKSON Leonard Eugene (1874-1954) en 1905.
Le premier corps non commutatif découvert, fut le corps des quaternions, par le mathématicien irlandais HAMILTON William Rowan (1805-1865) en 1843.
Théorème de WEIERSTRASS Karl Theodor Wilhelm (1815-1897)
Théorème de WEIERSTRASS. [AuCA] p 274, [Gour1] p 225
- L'espace des fonction polynômes est dense dans C( [a;b] , IK ) muni de la norme de la convergence uniforme.
ou - Toute fonction continue f de [a,b] ⊂ IR dans C est limite uniforme sur [a,b] d'une suite de fonctions polynômes
Histoire. [AuCA] p 274 et [Audi] p 364
En 1885, le mathématicien allemand WEIERSTRASS Karl Theodor Wilhelm (1815-1897) publie son théorème d'approximation polynômiale uniforme pour une fonction numérique continue sur un segment; théorème qui sera généralisé en 1937 par l'américain STONE Marshall Harvey (New York 1903).
STONE généralise ce théorème aux fonctionsà valeurs réelles ou complexes continue sur un compact..
Le théorème reste donc vrai si l'on remplace le segment [a,b] par une partie compacte de IR et même un compact quelconque d'un espace vectoriel normé.
Topologie
Définition. [Gour2] p 10 et p 9
La topologie est une science qui étudie les propriétés géométriques invariantes d'un objet quand celui-ci est étiré, tordu ou rétréci de manière continue.
Un espace topologique sur un espace métrique E est défini comme étant un ensemble muni d'une partie de P(E) dont les éléments sont appelés ouverts et vérifient les axiomes (1), (2) et (3).
- Axiome (1) : Les parties vides et E sont des ouverts.
- Axiome (2) : Une réunion d'ouverts est un ouvert.
- Axiome (3) : Une intersection fini d'ouverts est un ouvert.
Histoire. [HaSu] p223 et 210
C'est le mathématicien allemand, LISTING Johann Benedikt (1808-1882) qui introduit le terme topologie en 1847 mais il regrette de ne pouvoir utiliser le terme de géométrie de position (Geometrie der Lage), déjà utilisé par VON STAUDT pour désigner la géométrie projective.
Topologie est construit sur les racines grecques topos (espace, lieu) et logos (discours), science soit la science des lieux. Le mot topologie se diffuse peu hors d'Allemagne où on lui préfère le terme latin analysis situ (analyse de la position).
Pour se démarquer des études d'Oswald Veblen, le mathématicien américain d'origine russe LEFSCHETZ Solomon (1884-1972) reprend le mot allemand et l'anglicise en topology. L'importance de ses travaux popularise ce mot en anglais comme en français.
V.
Vecteurs.
Histoire. [Gueridon] p 106
En 1818, le mathématicien allemand MOBIUS August Ferdinand (1790-1868) introduit les calculs barycentriques qui préfigurent la notion de vecteurs.
En 1882, le mathématicien italien BELLAVITIS Giusto (1803-1880) introduit les vecteurs du plan.
A partir de 1845, le mathématicien anglais CAYLEY Arthur (Richmond 1821- Cambridge 1895), et les allemands GRASSMANN Hermann (1809-1877) et KRONECKER Leopold (1823-1891)utilisaient des vecteurs par leurs n coordonnées.
GRASSMANN étudia l'addition de ces vecteurs, leur indépendance linéaire, les sous-espaces et leurs dimension. Il donne en 1862 la formule : dim V + dim W = dim (V + W) + dim (V∩W).
La représentation axiomatique des espaces vectoriels réels et des applications linéaires de ces espaces est proposée en 1880 par l'italien PEANO Giuseppe (1858-1932).
Plus tard, le mathématicien allemand TOEPLITZ Otto (1881-1940) montrera que les démonstrations des principaux théorèmes relatifs aux espaces vectoriels peuvent se faire sans avoir recourt aux déterminants. On pourra ainsi étendre l'algèbre linéaire à un corps commutatif quelconque.
W.
Wronskien.
Définition. [AuCA] p457
La fonction W défini sur I par : W(t) = det ( Y1(t), ... , Yp(t) ) est appelé wronskien du système ( Y1(t), ... , Yp(t) )
où les fonctions Wi, sont des fonctions vectorielles définies sur un intervalle, et à valeurs dans IRp
Histoire. [HaSu]p371
Le mathématicien Français d'origine polonaise, WRONSKI Hoëné, Jozef Maria ( 1776 - Neuilly,France 1853) utilise dans un cours publié en 1812, le déterminant fonctionnel qui porte son nom, le Wronskien.
Z
Zêta (ou dzêta) fonction de Riemann.
Définition. [KoMe] p 105
Cette fonction est définie par : ζ (s) = ∑ 1/ns (pour n de 1 à + ∞) pour s réel ou complexe.
Propriétés. [KoMe] p 105
Si P désigne l'ensemble des nombres premiers, on a la relation : (Pour une démonstration voir [KoMe] p 105)
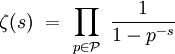
Histoire. [HaSu]p300, p160
RIEMANN Georg Friedrich Bernhard (1826-1866), dans ses travaux de 1859, il s'intéresse à la théorie des nombres.
Il étudie la fonction Zêta (ou dzêta) (qu'il baptise ainsi dès 1857, [Hauch]p222).
Il généralise alors cette fonction à la variable complexe. Pour tenter de démontrer la conjecture de TCHEBYCHEV sur la répartition des nombres premiers (cette conjecture deviendra lethéorème des nombres premiers, démontré par HADAMARD et DE LA VALLEE-POUSSIN en 1896), il étudie les zéros complexes de cette fonction.
Il émet alors l'hypothèse, qui porte le nom d'Hypothèse de Riemann, que tous les zéros imaginaires de la fonction ζ ont une partie imaginaire égale à 1/2. Cette hypothèse est encore ouverte en 2007 et fait partie des fameux problème de Hilbert (c'est le 8ème).
Euler ne parvient cependant pas à la démontrer (pas plus que la conjecture de TCHEBYCHEV).
Le mathématicien anglais HARDY Godfrey Harold (1877-1947) obtient son résultat le plus célèbre en 1914, en démontrant que a fonction Zêta de RIEMANN admet une infinité de zéros de partie réelle ½.




