Histoire et origine des symboles mathématiques
Je vous présente un petit résumé de l'apparition des différents symboles. Un développement est associé à certains symboles.
1 - Les opérations
-
Plus et moins + , −
WIDMANN (Allemagne), 1489 dans un traité d’arithmétique commerciale.
-
Multiplication : × et .
William OUGHTRED (1574-1660, Angleterre), en 1631 pour × et Gottfried Wilhelm Leibniz (1646 - 1716, Allemagne), en 1698 pour le point (.).
-
Division : Multiples symboles.
-
Exposants : Nicolas CHUQUET (15ème siècle), (mais généralisé bien après)
-
Le point pour le produit scalaire a été employé en 1902 dans Vector Analysis de J.W. GIBBS par E.B. Wilson.
-
× pour le produit de vecteurs a été employé en 1902 dans Vector Analysis de J.W. GIBBS par E.B. Wilson.
-
Plus-ou-moins (±) a été employé par William Oughtred (1574-1660) dans Clavis Mathematicae, édité en 1631.
-
Le symbole de produit (∏) a été introduit par René Descartes, selon Gullberg mais Cajori indique que ce symbole a été présenté par Gauss en 1812.
-
Racine carrée. √ par Christophe RUDOLFF (Allemagne), en 1525.
-
Addition ∑. Le symbole d'addition (∑) a été employé la première fois par Leonhard Euler (1707-1783) en 1755 :
"Signo de sumus de vsi de denotandam de differentiam d'annonce de Quemadmodum [lettre Delta en capital], signo d'indicabimus de summam d'ita (∑)."
Dans differentialis de calculi d'Institutiones ( 1755).
Ce symbole a aussi été employé par Lagrange, mais sa généralisation fut lente.
- Valeur absolue d'une différence.
Le tilde (˜) a été utilisé par William Oughtred (1574-1660) selon Smith, dans le Clavis Mathematicae, composé environ 1628 et édité à Londres en 1631. - Matrices.
En 1841, Arthur CAYLEY (1821-1895) a employé la notation moderne pour représenter le déterminante d'une matrice, une ligne verticale simple des deux côtés des nombres.
La notation est apparue dans le journal mathématique de Cambridge, vol. II (1841), P. 267-271. Cependant, Cayley a employé des virgules pour séparer des entrées dans des rangées (Cajori vol. 2, page 92).
=> Pour en savoir plus :
2 - Le symbolisme algébrique : utilisation des lettres
Maurolico, dit Francesco de Messina (début 16e) et François Viète (1540-1603, France) en sont les principaux acteurs.
3 - Les parenthèses (.)
Raphaël BOMBELLI (Bologne, 1522?-1572) (***)
4 - Les relations entres objets <, >, =, ≤ ≥
- ♠ Égalité = .
Robert RECORDE (1510-1558, Angleterre), en 1557. - <, > inférieur stricte, supérieur stricte.
Les symboles < et > apparaissent dans Artis Analyticae Praxis ad Aequationes Algebraicas Resolvendas de Thomas Harriot (1560-1621), publié de façon pasthume en 1631 :
"Signum majoritatis ut a > b significet a majorem quam b" and "Signum minoritatis ut a < b significet a minorem quam b." - ≤ ≥ , inférieur ou égal, supérieur ou égal.
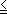
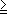 Pierre BOUGUER (1698-1758) utilise ces symboles en 1734.
Pierre BOUGUER (1698-1758) utilise ces symboles en 1734.
En 1670, John WALLIS utilise des symboles similaires avec une seule barre horizontale.
Le symbole actuel est sans doute le fruit d'une évolution typographique plus moderne. - ≠, différent de.
 EULER (1707 - 1783) utilise une graphie proche de celle usuelle (barre verticale pour EULER).
EULER (1707 - 1783) utilise une graphie proche de celle usuelle (barre verticale pour EULER). - ≈ presque égal.
Ce symbole a été employé en 1875 par Anton Steinhauser dans der Mathematik de Lehrbuch,« Algèbre ». Le même symbole a été employé en 1832 par Wolfgang Bolyai pour signifier l'égalité absolue.
5 - Constantes célèbres
- Pi : π
William JONES (1675-1749) en 1706 dans des mathesios de palmariorum de synthèse (⇒ développement) - e : exponentielle.
Cette constante, 2.71828…, a été mentionnée dans la traduction anglaise d'Edouard Wright du travail de NEPPER sur des logarithmes, éditée en 1618.
Le premier symbole utilisé pour la constante mentionnée par Cajori est la lettre b employée par Leibniz dans les lettres à Huygens en 1690 et 1691.
Leonhard Euler (1707-1783) a présenté e pour cette constante dans un manuscrit, Meditatio dans l'instituta de nuper de tormentorum d'explosione d'Experimenta (méditation sur des expériences faites récemment sur la mise à feu du canon), écrit à la fin de 1727 ou au début de 1728 (quand Euler avait juste 21 ans). Le manuscrit a été imprimé la première fois en 1862.
"Pour le nombre dont le logarithme est unité, laisser e être écrit, qui est 2.7182817… dont le logarithme [sic] selon Vlacq est 0.4342944…"
[traduit du latin par Florian Cajori].
Euler utilise ensuite e dans une lettre adressée à Goldbach le 25 novembre 1731, écrivant qu'e « dénote que le nombre dont le logarithme hyperbolique est égal à 1. »
Il apparait aussi dans Mechanica d'Euler (1736), dans lequel il a créé les bases de la mécanique analytique. - Le nombre d'or φ.
Selon les courbes de la vie : Étant un compte des formations en spirale et de leur application à la croissance en nature, à la Science, et à l'art : En se référant tout particulièrement aux manuscrits du da Vinci (1914) de Leonardo par monsieur Theodore Andrea Cook (1867-1928), page 420 :
"M. Mark Barr… suggéré… que ce rapport devrait s'appeler la proportion de phi pour des raisons données ci-dessous…. Le phi de symbole a été donné à cette proportion en partie parce qu'il a un bruit familier à ceux qui luttent constamment avec pi et en partie parce que c'est la 1ère lettre du nom de Pheidias, dans lequel la sculpture cette sculpture est vue pour régner quand la distance entre les points saillants sont mesurées."
- i pour l'imaginaire a été employé la première fois par Leonhard Euler (1707-1783) dans un mémoire présenté en 1777 mais non édité jusqu'en 1794 dans ses « integralis de calculi d'Institutionum. »
6 - Les nombres complexes ou imaginaires
- Imaginaire : DESCARTES (1596-1650), 1637
- Module : ARGAND (1768-1822, Suisse), 1806
- Argument : CAUCHY (1789-1857), 1838
- Nombre complexes : GAUSS (1777-1855), 1831
- Nombre N(z) carré du module : GAUSS(1777-1855), 1831
- Notation |z| pour le module : K.WEIERSTRASS (1815-1897)
- Notation i : EULER( 1707-1783), 1777, reprise par GAUSS(1777-1855)
- Représentation géométrique des complexes :
Le Danois WESSEL (1745-1818) en 1798 et le Suisse ARGAND (1768- 1822) en 1806 propose cette représentation, sans trop d'écho. C'est GAUSS (1777-1855) qui expose la théorie et CAUCHY (1789-1857) qui la diffuse. [DaDaPe] p125
7 - Les fonctions
=> Les notation fonctionnelles.
=> Histoire de la notion de fonction.
8 - La trigonométrie
Albert GIRARD (1595-1632) utilise les notations "sin, cos et tan" en 1626, dans Tables de sinus, tangentes et sécantes.
Mais c'est l'Allemand REGIOMONTANUS ( 15ème siècle) , qui est le créateur du mot sinus dans ses travaux sur la trigonométrie (De Triangulis omnimodus en 1464, publié en 1533)
Pour connaitre l'histoire de cette notion ⇒ La trigonométrie.
9 - Notation utilisées dans les calculs liés aux fonctions
-
Dérivation : dx, f '(x), u', Dx y
Les symboles dx, dy, and dx/dy sont introduits par Gottfried Wilhelm LEIBNIZ (1646-1716) dans un manuscript de 1675.
Les notations f '(x) pour la dérivée première, f ''(x) fpour la dérivée seconde, etc., sont introduites par Joseph Louis Lagrange (1736-1813). En 1797 dans Théorie des fonctions analytiques il utilisef'x et f''x.
Mais dans Nouvelle méthode pour résoudre les équations littérales par le moyen des séries (1770) il utilise la notation Ψ'.En 1772, le mathématicien français LAGRANGE Joseph Louis (1736-1813) écrit u' = du/dx et du = u'dx dans "Sur une nouvelle espèce de calcul relatif à la différentiation et à l'integration des quantités variables".
Dx y est introduit par Louis François Antoine ARBOGAST (1759-1803) dans "De Calcul des dérivations et ses usages dans la théorie des suites et dans le calcul différentiel," (1800).
Il fut aussi utilisé par Jean BERNOULLI.
-
Dérivée partielle : ∂
Le symbole ∂ est utilisé en 1770 par CONDORCET Marie Jean Antoine Caritat de (1743-1794) dans "Memoire sur les Equations aux différence partielles," publié dans Histoire de L'Academie Royale des Sciences (1773).
Cependant le ∂ fut pour la première fois utilisé par Adrien-Marie LEGENDRE (1752-1833) en 1786 dans "Memoire sur la manière de distinguer les maxima des minima dans le Calcul des Variations".
LEGENDRE abandonne cette notation par la suite, elle est réintroduite par Carl Gustav Jacob JACOBI en 1841 dans De determinantibus Functionalibus" publié dans le Journal de Crelle en 1841.
Pour en savoir plus, voir la page sur les fonctions de plusieurs variables. -
Le symbole intégral : ∫
Leibniz écrivait omn. pour "omnia" avant le terme à intégrer.
Le symbole intégral : ∫ fut pour la première fois utilisé par le mathématicien Gottfried Wilhelm LEIBNIZ (1646-1716) en, 1675, dans un traité non publié. Il plaça ensuite le symbole dx après l'intégrande.
En 1675, il en propose l'usage dans une lettre à Henry Oldenburg, secretaire de la Royal Society :
"Utile erit scribi ∫ pro omnia, ut ∫l = omn. l, id est summa ipsorum l"
Sa première apparition vient ensuite dans un papier de Leibniz, Acta Eruditorum.
Ce symbole vient d'une déformation du S de Summa. -
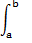 Au début les bornes d'intégration sont indiquées par des mots. EULER est le premier à utiliser un symbole dans Institutiones calculi integralis, il place les bornes dans des parenthèses.
Au début les bornes d'intégration sont indiquées par des mots. EULER est le premier à utiliser un symbole dans Institutiones calculi integralis, il place les bornes dans des parenthèses. -
Le symbolisme actuel est initié par Jean Baptiste Joseph Fourier (1768-1830), en 1822 dans The Analytical Theory of Heat.
-
La limite : lim
La notaion lim, est introduite par le suisse Simon-Antoine-Jean LHUILIER (1750-1840) en 1786 et par Karl Weierstrass (1815-1897) en 1841 dans un de ses papiers publiés en 1894 dans les Mathematische Werke. [HaSu] p 217 et [Cajo].
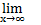 La notation avec une flêche est introduite par Godfrey Harold Hardy (1877-1947) dans "A Course of Pure Mathematics, publié en 1908.
La notation avec une flêche est introduite par Godfrey Harold Hardy (1877-1947) dans "A Course of Pure Mathematics, publié en 1908.
-
Le symbole infini : ∞
Ce symbole ∞ est proposé par John Wallis (1616-1703) en 1655 dans De sectionibus conicis. -
Les symboles grecs delta et epsilon : δ , ε
En 1706, Jean BERNOULLI utilise δ tpour désigner une différence (petite).
Augustin-Louis Cauchy (1789-1857) utilise ε en 1821 dans son Cours d'analyse, et parfois δ à sa place.
"δ viendrait de d de 'différence' et ε du e d' 'erreur' selon certains spécialistes.
Il utilise ces symboles dans ces démonstrations comme nous le faisons actuellement.
10 - Notations liées aux probabilités et statistiques
-
Factorielle : n!
Par Christian KRAMP (1760-1826) en 1808 dans Élémens d'arithmétique universelle (1808).
-
Permutations et combinaisons : Cnp = ( pn) et An p
La notation modernes avec parenthèses apparait en 1826 dans Die Combinatorische Analyse de l'allemand ETTINGSHAUSEN Andreas von (1796 - 1878) et dans Vorlesungen über höhere Mathematik, Vol. I.
Harvey GOODWIN (1818 - 1891) utilise nPp pour le nombre d'arrangements de p éléments parmis n en 1869 dans Elementary Course of Mathematics.
G. CHRYSTAL (1851 - 1911) utilise nCp pour le nombre de combinaisons de p éléments parmi n dans Algebra, Part II (1899), ouvrage que l'on peut consulter en ligne sur le site onlinebooks.
Pour connaitre l'histoire des probabilités =>
11 - Les ensembles de nombres
-
IN : Origine du symbole IN, pour les entiers natiurels (de naturale en italien)
Le mathématicien italien PEANO Giuseppe (1858-1932) définit l'ensemble des entiers naturels non nuls par des axiomes qui portent aujourd'hui son nom et le note N ( Il deviendra ensuite IN pour désigner l'ensemble des nombres naturels). [HaSu] p276.
CAJORI précise que :
En 1895 dans Formulaire de mathématiques, PEANO utilise N pour les entiers positifs non nuls, n pour les entiers (relatifs) , N0 pour les entiers positifs (avec 0), R pour les nombres rationnels positifs, r pour les nombres rationnels, Q pour les nombres réels positifs non nuls, q pour les nombres réels, et Q0 pour les nombres réels positifs (avec 0). [Cajo] vol. 2, page 299].
L'expression nombre naturel apparaît vers 1675, à l'époque où les nombres négatifs sont enfin accéptés. [Hauch] p 132
-
ID : Origine du symbole ID, Ensemble des décimaux : notation française du groupe BOURBAKI en 1970.
-
Q : Origine du symbole Q, Ensemble des nombres rationnels.
Le mathématicien italien PEANO Giuseppe (1858-1932) aurait utilisé la lettre Q, première lettre de quotiente mais, selon plusieurs sources, pas pour désigner l'ensemble des rationnels. Cette notation viendrait en fait du groupe BOURBAKI dans Algèbre, Chapitre 1. (1969)
Le mot rationnel apparaît en mathématiques vers 1550 (en même temps que le terme irrationnel). Un nombre irrationnel est aussi appelé à l'époque nombre sourd. Il semblerait que cela vienne d'une mauvaise traduction des mots rationnel et irrationnel en arabe à l'époque du célèbre mathématicien perse KHWARIZMI Mohammed Ibn musa AL ( khiva 788 - Bagdad 850).
-
Z : Origine du symbole Z, Ensemble des nombres relatifs.
Cette notation viendrait en fait du groupe BOURBAKI dans Algèbre, Chapitre 1. (1969)
La lettre viendrait de Zahl (nombre) et zahlen (compter) de l'allemand.
DEDEKIND Julius Wilhelm Richard (1831-1916) et CANTOR Georg (1845-1918) sont souvent cités mais il semble que le premier utilisait K pour les entiers et J pour les complexes (selon les historiens Walter Felscher, Stacy Langton, Peter Flor, et A. J. Franco de Oliveira).
-
IR : Origine du symbole IR, Ensemble des nombres réels. ℜ
Les origines de l'utilisation de la lettre R puis IR pour désigner l'ensemble des réels sont multiples.
Contrairement à ce que l'on lit souvent, CAJORI affirme que DEDEKIND Julius Wilhelm Richard (1831-1916) utilise R pour les rationnels et le R gothique, ℜ , pour les réels dans Stetigkeit und irrationale Zahlen (1872).
-
C : Origine du symbole C, Ensembles des nombres complexes ou imaginaires.
L'origine du symbole C pour désigner l'ensemble des nombres complexes est assez récente. On trouve selon l'historien des mathématiques William C. Waterhouse (en 2001) ce symbole dans les papiers de JACOBSON Nathan (1910 - 1999), Structure and Automorphisms of Semi-Simple Lie Groups in the Large, (1939).
La seconde édition de Survey of Modern Algebra (1953) de Birkhoff and MacLane, utilise aussi C (mais J pour les entiers, R pour les rationnels, R# pour les réels).
Le groupe BOURBAKI l'utilise aussi dans ses travaux de 1969 et participe à sa généralisation.
12 - Les matrices
Voir la page sur l'histoire de la notion de matrice.
13 - Notations ensemblistes et logiques : ∈ ; ∩ ; ∪ ; ⊂ ; ⊃
- Origine des symboles intersection et union : ∩ et ∪
Les symboles ∩ and ∪ sont utilisés pour la première fois par le mathématicien allemand GRASSMANN Hermann (1809-1877) dans Die Ausdehnungslehre von (1844) mais il les utilise comme symbole d'opération, pas nécessairement pour désigner l'union et l'intersection.
Puis c'est le mathématicien italien PEANO Giuseppe (1858-1932) qui les utilise à cet usage en 1888 dans Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann ([Cajo] page 298).
- Histoire du symbole "il existe" : ∃
C'est le mathématicien italien PEANO Giuseppe (1858-1932) qui utilise le symbole ∃ dans Formulaire de mathematiqués, en 1897.
- Histoire du symbole "appartient à" : ∈.
Le mathématicien italien PEANO Giuseppe (1858-1932) utilise le symbole ε (epsilon) dans ses Arithmetices prinicipia nova methodo exposita, en 1889 et dans Formulaire de mathematiqués, en 1897, pour désigner l'appartenance à un ensemble. Cela viendrait en fait de la première lettre du mot grec qui signifie est.
Le symbole ∈ pour désigner l'appartenance apparaitrait dans le traité du mathématicien anglais RUSSELL Bertrand Arthur William (1872-1970), Principles of Mathematics en 1903.
- Histoire du symbole "pour tout ou quelque soit" : ∀.
CAJORI, insiste sur le fait que l'italien PEANO Giuseppe (1858-1932) utilise le symbole ∀(pour tout) avant l'anglais RUSSELL Bertrand Arthur William (1872-1970).RUSSELL utilisait la notation (x) signifiant "pour tout x".
-
Histoire du symbole "ensemble vide" : Ø.
Ce symbole pour désigner l'ensemble vide apparait dans les travaux du groupe BOURBAKI Éléments de mathématique Fasc.1: Les structures fondamentales de l'analyse; Liv.1: Théorie des ensembles. (Fascicule de resultants) (1939): "certaines propriétés... ne sont vraies pour aucun élément de E... la partie qu’elles définissent est appelée la partie vide de E, et designée par la notation Ø."Le mathematicien français André WEIL (1906-1998), membre du groupe BOURBAKI, se dit responsable de l'introduction de ce symbole.
-
Histoire du symbole "équivaut à" : ↔ et ⇔ .
Le symbol ↔ pour désigner une équivalence logique apparait en 1936 dans le traité du mathématicien allemand Wilhelm Ackermann (1896 - 1962) Die Widerspruchsfreiheit der allgemeinen Mengenlehre.La double flêche ⇔ est utilisée en 1954 par les BOURBAKI dans Theorie des ensembles, 3. edition, Paris, 1954.
Tableaux Synoptiques
17ème siècle.
|
(Le point .) |
William OUGHTRED (1574-1660, Angleterre), en 1631 Gottfried Wilhelm Leibniz (1646 - 1716, Allemagne), en 1698 |
|
infini ∞ |
John WALLIS (1616-1703, Angleterre) |
| ab |
La barre de fraction horizontale a été introduite par les Arabes. "Les Arabes ont d'abord copié la notation hindoue, mais l'ont ensuite améliorée en insérant une barre horizontale entre les deux nombres" (Burton). Plusieurs sources attribuent la barre de fraction horizontale à al-Hassar vers 1200. Lorsque Rabbi ben Ezra (vers 1140) a adopté les formes mauresques, il a généralement omis la barre. Fibonacci (vers 1175-1250) a été le premier mathématicien européen à utiliser la barre de fraction telle qu'elle est utilisée aujourd'hui. Il a suivi la pratique arabe consistant à placer la fraction à gauche du nombre entier (Cajori vol. 1, page 311). (source) |
|
a/b (quotient) avec barre |
La barre de fraction diagonale (également appelée solidus ou virgule) a été introduite parce que la barre de fraction horizontale était difficile à utiliser du point de vue typographique, car elle nécessitait trois terrasses de caractères. L'exemple le plus ancien de barre de fraction diagonale montré par Cajori (vol. 1, page 313) date de 1784, lorsqu'une ligne courbe ressemblant au signe d'intégration a été utilisée dans les Gazetas de Mexico par Manuel Antonio Valdes. |
|
π (Pi) |
William OUGHTRED (1574-1660, Angleterre) pour désigner le périmètre d'un cercle mais c'est l'anglais William JONES qui utilise ce symbole pour la première fois en 1706 pour désigner le rapport du périmètre sur son diamètre. L'utilisation est développée par Euler. [HaSu] p185. |
|
∫(intégrale) |
LEIBNIZ (1646, 171) |
|
dx (notation différentielle) |
LEIBNIZ (1646, 1716) |
|
< et > |
Thomas HARRIOT (1560-1621, Angleterre), en 1630 et Albert GIRARD (1595-1632) (*) |
|
point décimal, virgule décimale |
STEVIN (1548-1620), SNELLIUS |
|
sin, cos et tan |
Albert GIRARD (1595-1632) (*) |
|
÷ |
PELL John (1610 - Londres 1685) édite l'algèbre de RHONIUS ( ou Johann Rahn (1622-1676), Teutsche Algebra, 1659) qui contient pour la première fois le symbole ÷ utilisé pas les anglo-Saxons pour la division. [HaSu] p279 |
18e siècle
| a.b (produit scalaire) | WILSON (1741-1793)/GIBBS (1839-1903, USA) |
| e | Léonhard EULER ( Bâle, 1707-1783) |
| f(x) | Léonhard EULER ( Bâle, 1707-1783) |
| Le signe Σ | Léonhard EULER ( Bâle, 1707-1783) (*) |
| f'(x) (dérivée) | LAGRANGE (1736-1813) |
| Les indices | Gabriel CRAMER (1704-1752, Suisse) en 1750 (les ','',''' suivis par iv , v, etc. deviennent usuels à la même époque) (*) |
19e siècle
| CAUCHY (1789-1857) | |
| ARGAND (1768-1822, Suisse) | |
| Adrien-Marie LE GENDRE (Paris 1752-1833) | |
| n! (= 1x 2x 3x ... xn , factorielle) | KRAMP (1760-1826) |
20e siècle
| a ^ b (produit vectoriel) | BURALI-FORTI (1861-1931,Italie) / MARCOLONGO. Aux USA la croix (x) instituée par GIBBS (1839-1903, USA) ou les crochets [u,v] sont plutôt utilisés. |
| BOURBAKI (20e siècle) | |
| ( |
BOURBAKI (20e siècle) |
| || x || (norme) | Fréchet (1878-1973) |
| f : A |
Fréchet (1878-1973) |
| PEANO (1858-1932)/ FREGE | |
|
A - B (différence symétrique),
|
PEANO (1858-1932) |
| (quel que soit) : |
HILBERT (1862-1943) |
| France, dans les années 1930. Voir aussi STEVIN. |
Bibliographie :
- La référence de base est : [Cajo] : Florian CAJORI, History of mathematicals notations, Thèse de réf. 01-1 CAT.74.
Mais on trouve certaines remarques intéressante dans les ouvrages suivants :
- [Esco] : Jean-Pierre ESCOFIER, Théorie de Gallois, Masson, Paris, 1997. page 6
- [HaSu] : B. Hauchecorne et D. Surateau, Des mathématiciens de A à Z, Ellipse, Paris, 1996.
- (*) [Guedj1] : Denis GUEDJ, Le théorème du perroquet, Seuil page 249
- (**) [Audi] : J.L.AUDIRAC, Vie et œuvre des grands mathématiciens, Magnard, Paris, 1990. page 34
- (***) [DaDaPe] : A.DAHAN-DALMEDICO/J.PEIFFER, Une histoire des mathématiques, Seuil, Paris, 1986. page 262



