 ARCHIMÈDE
ARCHIMÈDE
Naissance: vers 287 av. J.-C. à Syracuse, Sicile - Mort : 212 av. J.-C. à Syracuse, Sicile
Sa vie.
1. Archimède, en bref.
Né vers 287 avant JC à Syracuse, il serait le fils de l'astronome Phidias (pas le sculpteur qui lui, vécu au 5ème siècle av. J.-C.), dont il fait une brève allusion dans son traité "l'Arénaire".
Archimède passe son enfance à Syracuse et très tôt se rend à Alexandrie pour apprendre auprès d'Euclide (3ème av. J.-C.).
Dans cette célèbre ville qui fut le siège du savoir antique, il rencontre Ératosthène (3ème av. JC), le conservateur de la grande bibliothèque.
Après des voyages en Égypte et en Espagne, il s'installe définitivement à Syracuse.
Protégé par le souverain et mis à l'abri des soucis matériels, il peut alors se consacrer à ses recherches scientifiques.
Le gouvernement lui demande alors souvent conseil pour résoudre des problèmes techniques.
Archimède est, avec Euclide, le plus grand mathématicien de l'antiquité.
Ses découvertes sont connues par des lettres qu'il adresse aux mathématiciens de l'époque.
2. Son apport scientifique : Ses traités.
2a. Archimède, mathématicien.
Archimède est avant tout un géomètre.
2a-1. Approximation du nombre pi.
Dans son ouvrage "Mesure du cercle", il élabore une méthode permettant de donner une approximation précise de pi (π).
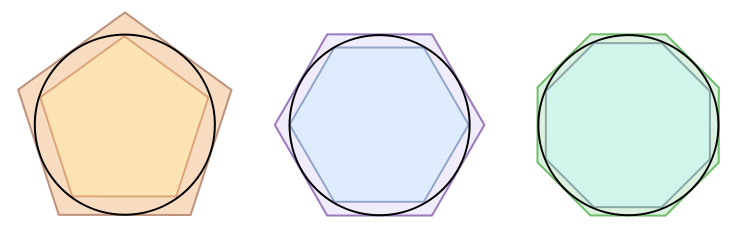
En utilisant des polygones réguliers de 96 côtés circonscrits et inscrits dans le cercle, il parvient à démontrer que pi est compris entre 22/7 et 223/71.
Il élabore en outre des tables de sinus (cf. aussi, histoire de la trigonométrie).
2a-2. Paraboles, sphère, cylindres et quadratures.
Archimède étudie les coniques et propose des quadratures originales de la parabole.
Il calcule l'aire délimitée par un arc de parabole et la corde qui le soutend par une technique de calcul utilisant une série convergente, technique de calcul très avancée pour l'époque. Il étudie les solides engendrés par la rotation des coniques autour de leurs axes. Il donne la formule du volume de la sphère et du cylindre ainsi que leurs aires. Il formula à ce titre la demande que soient gravées sur sa tombe ces formules.
Dans son traité sur les sphéroïdes et sur les conoïdes, il étudie les paraboloïdes et les ellipsoïdes. De plus, ses travaux sur les tangentes et les quadratures l'amènent à envisager le calcul différentiel et intégral.
Une courbe, « la spirale d'Archimède», porte son nom. C'est une courbe d'équation polaire ρ = a. θ.
2a-3. Archimède et l'arithmétique.
Ses travaux en arithmétique sont exposés dans deux lettres dont la première est malheureusement perdue.
Ces missives traitent de la numération, en particulier de l'expression de grands nombres.
Il améliore le système numérique grec ( ⇒ voir la page numération grecque), en y introduisant les exposants afin de représenter les grands nombres.
La numération grecque ne permettait pas de dépasser 108.
Il considère alors ce nombre comme une unité, il peut ensuite écrire des nombres jusqu'à 1016 qu'il considère comme un nombre de deuxième espèce etc.
Avec cette méthode, il estime que le nombre de grains de sable que l'on peut mettre dans l'univers est de 1051,
soit " 1000 unités du septième ordre de nombres " .
Un calcul simple montre que, si l'on considère des grains de sables sphériques de 0,1 mm de rayon, empilés dans une sphère, on englobe l'orbite de toutes les planètes, mais pas encore celles des comètes. Archimède était resté à l'intérieur du système solaire.
On considère actuellement que le nombre d'atomes de l'univers est de l'ordre de 1080
2a-4. Archimède et les suites.
En outre il met en rapport pour la première fois, deux suites, l'une arithmétique et l'autre géométrique.
C'est précisément cette méthode que perfectionnera le baron de Merchiston, John Napier, plus connu sous le nom francisé de Neper (1550-1617) , avec les logarithmes dits népériens.
2a-5. Ensemble archimédien.
L'axiome d'Archimède est une formulation antique d'axiomes dits de continuité.
C'est une propriété utilisée dès l'Antiquité. L'axiome s'applique aux grandeurs ayant une raison entre elles, ce qui, selon le livre V des Eléments d'Euclide, signifie :
Des grandeurs sont dites avoir une raison entre elles lorsque ces grandeurs, étant multipliées, peuvent se surpasser mutuellement.
Il précise que :
Il y a toujours un multiple du plus petit qui est supérieur au plus grand.
Si l'on a 2 segments, on peut toujours, en multipliant le petit, dépasser le grand.
On dit alors que le corps IR est archimédien pour rendre homage à l'illustre scientifique, cendant, il l'attribue à EUDOXE de Cnide (-408 — -355 ou -395 — -342) qui l'aurait énoncée un siècle auparavant.
2b. Archimède le physicien.
Archimède est aussi un brillant physicien.
- La vis sans fin.
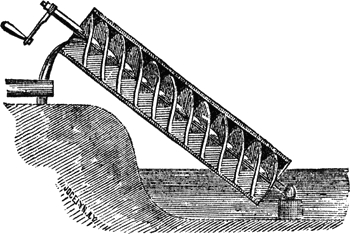
En mécanique, il est l'inventeur d'un dispositif permettant aux habitants du bord du nil, d'arroser leurs terrains, la vis sans fin (ou vis d'Archimède).
C'est cet appareil élévatoire d'eau, qu'une fresque récemment mise à jour à Pompéi montre mue par le pied d'un esclave.
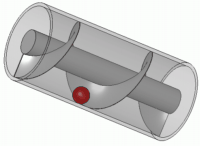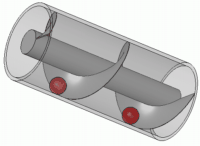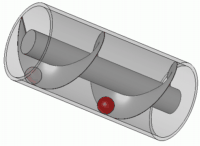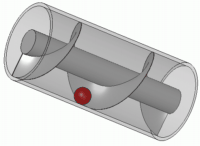
- La roue dentée.
On lui doit aussi le boulon formé d'une vis et d'un écrou ainsi que la découverte de la roue dentée.
C'est grâce à celle-ci qu'il construit un planétaire représentant l'Univers connu à l'époque.

Mais c'est avant tout par ses recherches en statique et en hydrostatique qu'Archimède se distingue.
- La théorie du levier.
Dans son traité "de l'équilibre des figures planes", il expose sa théorie du levier (deux corps s'équilibrent à des distances inversement proportionnelles à leur poids) et introduit la notion de centre de gravité. Il détermine notamment les barycentres de plusieurs figures géométriques.
Cette découverte fait l'objet d'une anecdote rendue célèbre par Plutarque (40 ap. JC - 120 ap. JC).
« Archimède avança un jour au roi Hiéron, dont il était le parent et l'ami, qu'avec une force donnée on pouvait remuer un fardeau de quelque poids que ce fût.
Plein de confiance sur la force de sa démonstration, il se vante que s'il avait une autre terre, il remuerait à son gré celle-ci en passant dans l'autre.
Le roi étonné de cette assertion, le pria de réduire en pratique son problème. Et de lui faire voir une grande masse remuée par une petite. Archimède ayant fait tirer à terre, avec un grand travail et force de bras, une des galères du roi, ordonna qu'on y mit la charge ordinaire avec autant d'hommes qu'elle pouvait contenir. »
- Tout corps plongé dans un liquide...
Enfin, dans son traité longtemps perdu, "Des corps flottants", il élabore la célèbre loi :
"tout corps plongé dans un fluide subit une poussée verticale, dirigée de bas en haut, égale au poids du fluide déplacé " ,
que l'on nomme communément "poussée d'Archimède".
Pendant longtemps on cherchera en vain ce manuscrit, jusqu'à cette incroyable découverte en 1899.
Cette année-là, un paléographe nommé Papadopoulos Kerameus furetant dans les archives du patriarcat grec de Jérusalem, met la main sur un palimpseste, (du grec ancien, "gratté de nouveau").
Un palimpseste est un parchemin ancien, lavé et réutilisé, montrant des traces d'un traité de mathématiques et la paléographie (du grec palaios, « ancien » et graphein, « écrire ») est l'étude des écritures manuscrites anciennes, indépendamment de la langue utilisée.
Papadopoulos Kerameus publie sa découverte, qui reste ignorée quelques années, jusqu'à ce qu'en 1906, Heiberg, révèle qu'il contient trois textes d'Archimède : le Stomachion, la Méthode, et le Traité des corps flottants.
Les deux premiers étant absolument inconnus, le troisième inédit dans sa version grecque.
Il s'avéra que leur transcription remontait au Xème siècle, et leur tentative d'effacement, du XIIème au XVème siècle.
2c. Ses traités.
Au total, ce sont douze traités qui nous sont parvenus mais on suppose généralement qu'il en écrivit bien plus d'autres.
- De l'équilibre des figures planes, livre I.
- De l'équilibre des figures planes, livre II.
- De la sphère et du cylindre, livres I et II.
- De la mesure du cercle.
- L'arénaire.
- La catoptrique
- De la méthode.
- La Quadrature de la parabole.
- Des spirales.
- Sur les conoïdes et les sphéroïdes.
- Des corps flottants, livres I et II.
2d. Eurêka !
La légende veut que le tyran de Syracuse, Hiéron II (270 av. JC - 215 av. JC), ait demandé au savant de savoir si la couronne fabriquée à sa demande était faite d'or pur ou d'un alliage d'or et d'argent.
En réfléchissant au problème dans son bain, Archimède fut frappé par la diminution de poids de ses membres dans l'eau. Il comprit alors que cette perte de poids correspondait au poids de l'eau déplacée et, dans l'enthousiasme de sa découverte, s'élança nu dans la rue en criant " Eurêka ! Eurêka ! " (j'ai trouvé) .
On ne sait cependant ce qu'il advint du joaillier truqueur.
3. Archimède le stratège : La défense de Syracuse.
En 215 av. J.-C., Archimède organise la défense de Syracuse face à l'invasion des Romains et du général Marcellus lors de la seconde guerre punique au cours de laquelle les habitants de Syracuse s'étaient alliés aux Carthaginois, après avoir été les alliés de Rome pendant près d'un demi-siècle.
Durant trois ans, il fait construire des machines de guerre afin de résister aux galères romaines qui font face à Syracuse.
Anthemius de Tralles (474 - 534) - dont les écrits contestés irritèrent Descartes (1596 - 1650) - fait le récit de l'utilisation par Archimède, de Catapultes et de miroirs ardents, lors de cette bataille légendaire.
Tite-Live (59 av. JC - 17 ap. JC) raconte :
"Un levier, établi au-dessus du mur, lançait sur la proue de ses vaisseaux une main de fer attachée à une forte chaîne. Un énorme contrepoids en plomb ramenait en arrière la main de fer qui enlevait ainsi la proue, suspendait le vaisseau droit sur sa poupe; puis le rejetait de telle sorte qu'il paraissait tomber du mur....."
- La controverse des miroirs ardents.
Peinture murale de Stanzino delle Matematiche à la Galleria degli Uffizi (Florence, Italy).
Par Giulio Parigi (1571-1635) en 1599-1600.
Si la légende est belle, beaucoup de scientifiques dont Descartes (1596 - 1650) s'accordent à penser que les faits sont peu vraisemblables.
La question, aujourd'hui encore, n'est pas absolument éclaircie. Mais les experts font généralement preuve de scepticisme.
En 1977, le dossier a été une nouvelle fois examiné par un spécialiste des phénomènes de combustion, l'Anglais D. L. Simms.
D'après lui, le doute n'est pas permis : non seulement les preuves historiques sont fragiles, mais il est scientifiquement et techniquement impossible que cet exploit ait pu être réalisé.
Au IIIème siècle avant Jésus-Christ, il affirme qu'il est invraisemblable qu'Archimède ait eu les connaissances et les moyens matériels nécessaires.
Autrement-dit, l'expertise technologique confirmerait sans ambiguïté le verdict défavorable de nombreux historiens : l'épisode des miroirs d'Archimède serait un mythe inventé de toutes pièces.
La question technique, demeure ouverte.
Rien n'empêche de croire qu'Archimède, avec des miroirs métalliques par exemple, ait été en mesure d'obtenir de bons résultats.
Cette supposition a été assez bien confirmée, en 1973, par une expérience, due à Ioannis Sakkas, un ingénieur grec.
Comme miroirs, il a utilisé des surfaces ayant en principe des dimensions comparables à celles des boucliers grecs classiques (environ 1,70 m sur 0,70 m).
Pour ne pas trop s'éloigner de la réalité historique, il a même pris soin de modifier la surface de ses panneaux de glace en les recouvrant d'une mince pellicule de bronze pas trop bien polie.
Ayant ainsi préparé soixante-dix « boucliers-miroirs », il les a confiés à des aides qui, au Pirée, concentrèrent les rayons solaires sur le modèle réduit d'une galère (longueur : 3,60 m) qui flottait à une cinquantaine de mètres.
En deux minutes, la cible prit feu ; et ce de façon assez intense.
D. L. Simms lui-même semble admettre qu'à Syracuse, avec un beau soleil, l'effet aurait pu être plus rapide. La conclusion, c'est que des moyens modestes permettent d'obtenir des résultats assez spectaculaires. L' expérience d'Archimède n'est peut-être pas un miracle.
Mais D. L. Simms ne s'avoue pas vaincu. Brûler une cible fixe est envisageable mais il faut qu'elle soit exactement située au « foyer» du miroir. Mais ce n'est pas vraiment le cas d'une galère qui peut se déplacer à sa guise (enfin si les rameurs y consentent).
Alors puisqu'on ne peut vraiment démontrer qu'Archimède n'a pas pu réaliser de tels exploits, accordons un peu de crédit à cette jolie légende !

5. La mort d'un génie.
Cependant, la ville est finalement envahie et Archimède est tué lors des combats, à 75 ans !.
Selon le biographe Plutarque (40 ap. JC - 120 ap. JC), un soldat romain croisa Archimède alors que celui-ci traçait des figures géométriques sur le sol. Troublé dans sa concentration par le soldat, Archimède lui aurait lancé « Ne dérange pas mes cercles !», citation restée célèbre.
Le soldat vexé par le vieillard de 75 ans, l'aurait alors tué d'un coup d'épée. En hommage à son génie, Marcellus lui fit de somptueuses funérailles et fit dresser un tombeau décoré de sculptures représentant une sphère et son cylindre circonscrit.
Une gravure d'après un tableau du peintre Gustave Courtois (1853-1923).





