 THALÈS de Milet
THALÈS de Milet
Naissance: vers 624 av. J.-C., Asie Mineur (Turquie) - Mort: vers 547 av. J.-C. à Milet, Asie Mineur (Turquie)
Sa vie.
1. Le contexte.
Au VII siècle avant notre ère, sur les côtes de l'Anatolie, alors qu'à Sardes, la capitale de l'empire de Lydie, règne le fils du roi Gugu, en Ionie toute proche, aucun roi ne règne sur Milet. La ville est l'une des première cités-États.
Thalès, au dire d'Hérodote (484 av. JC - 425 av. JC), de Douris (340 av. JC - 270 av. JC) et de Démocrite (470 av. JC - 370 av. JC), était fils d'Examios et de Cléobuline, et membre de la famille des Thélides, des rois mythiques de Phénicie de la lignée d'Agénor et de Cadmos, s'il faut en croire Platon.
Le premier, il porta le nom de sage, au temps où Damasias était archonte à Athènes (nom donné dans la plupart des cités grecques, aux titulaires des charges les plus élevées, qui avaient d'importantes fonctions judiciaires et politiques).
C'est sous le même archontat que fut créée l'expression : « les sept sages » .
Thalès fut inscrit comme citoyen de Milet quand il vint dans cette ville avec Nélée chassé de Phénicie. Une autre tradition très courante veut qu'il soit natif de Milet et qu'il descende d'une bonne famille. Il s'occupa de politique avant d'étudier la nature.
2. Thales, en bref
Thalès de Milet serait un commerçant suffisamment riche, pour se permettre de consacrer sa vie aux voyages et aux études.
En Egypte, il aurait mesuré les grandes pyramides grâce à leur ombre et à "son" fameux théorème. De retour à Milet, il devient homme politique, homme d'affaires et philosophe.
Ses travaux portent sur les mathématiques (six résultats importants lui sont attribués), l'astrologie (éclipses) et la philosophie (tout vient de l'eau).
- Selon ARISTOTE, il est le premier spéculateur de l'histoire. Une année de récolte d'olives importante, il aurait acheté toute celle produites dans sa région et les aurait revendues petit à petit, pour éviter une chute massive des prix, (et se faire beaucoup d'argent !).
Sa mort reste aussi, assez mystérieuse.

3. Thales et l'astronomie
Thalès ne laissa aucun écrit, et même l'Astrologie nautique écrite en vers qu'on lui attribue est de Phocos de Samos. Cela rend donc difficile la réalisation d'une biographie incontestée de ce sage.
Cependant beaucoup d'historiens antiques citent Thalès en faisant montre d'un respect certain.
- Hérodote (484 av. JC - 425 av. JC), et Pline l'Ancien (23 ap. JC - 79 ap. JC), s'accordent sur la prédiction d'une éclipse totale de Soleil par Thalès.
Celle-ci, perçue comme un présage des Dieux, aurait mis fin à la guerre entre les Mèdes et les Lydiens le 28 mai 585 av. JC, après une bataille que l'on nomme encore "Bataille de l'éclipse". - D'après Diogène Laërce (IIIe siècle), après avoir exercé une carrière politique il se serait intéressé à la science de la nature.
- Certains attribuent également à Thalès deux autres ouvrages intitulés Sur les solstices pour le premier et Sur les équinoxes pour le second.
Il semble cependant avéré qu'il soit le premier véritable astronome grec.
- Hésychius d'Alexandrie (VIe siècle), tout comme Eudème, écrit que Thalès, le premier, découvrit le passage du Soleil d'un tropique à l'autre.
- Selon un texte de Diogène Laërce (IIIe siècle), il aurait également essayé de calculer la dimension du Soleil et de la Lune.
Ce qui semble certain c'est que c'est avec Thalès de Milet que commença réellement l'aventure scientifique de l'étude de la nature. Il aurait étudié la géométrie en Égypte et aurait mesuré la hauteur d'une pyramide par la longueur de son ombre.
- Callimaque de Cyrène (IIIe av. JC), dans ses Iambes, croit qu'il découvrit la Petite Ourse et le raconte en vers iambiques :
Il mesura, dit-on, les étoiles du Chariot
Sur quoi les Phéniciens règlent leur navigation.
4. La philosophie de Thales
Sa cosmogonie pourrait elle se réduire à ces points :
- De toutes choses était l'eau,
- le monde était animé et plein de démons.
5. Thales précurseur
5.a. Le premier penseur
Thalès a été le premier "penseur" de l'histoire, il a posé et s'est posé des questions, par exemple :
- qu'est-ce que penser ?
- Quels liens y a-t-il entre ce que je pense et ce qui est ?
- De quoi est faite la nature ?
A son époque, au 6e siècle avant notre ère, philosophie et mathématiques, étaient totalement imbriquées si l'on peut dire car ces mots n'existaient pas encore (cf. étymologie).
Selon certaines sources (cf. [Guedj1]) on lui doit la célèbre formule : "connais-toi toi-même !". Pourtant nombreux sont ceux qui l'attribuent à Socrate (5ème siècle av. J.-C.)
Il fut l'un des 7 Sages de la Grèce antique, et le premier à énoncer des résultats généraux concernant les objets mathématiques.
5.b. Le premier mathématicien.
Thalès ne s'est pas beaucoup occupé des nombres, il s'est surtout intéressé aux figures géométriques, cercles, droites, triangles.
Il fut le premier à considérer l'angle comme un être mathématique à part entière et il en fit la 4e grandeur géométrique (longueur, surface, volume, angle).
La grande innovation de Thalès réside dans le fait qu'il affirme des vérités, non pas à partir d'un objet singulier, comme c'était le cas avant lui pour les Égyptiens ou les Babyloniens, mais pour une infinité d'objets du monde.
Son ambition, d'une nouveauté absolue, est d'émettre des vérités concernant une classe entière d'êtres.
Pour pouvoir y parvenir, Thalès va être obligé, par sa seule pensée, de concevoir un être idéal, "le cercle", qui est en quelque sorte le représentant de tous les cercles du monde.
De ce fait une phrase comme :
"toute droite passant par le centre d'un cercle le coupe en deux parties égales"
est alors révolutionnaire. C'est en ce sens que l'on peut lui attribuer le titre de premier mathématicien de l'histoire.
6. Son apport mathématique
- Thalès affirma que les angles opposés par le sommet formés par deux droites qui se coupent sont égaux.
- Thalès a montré qu'à chaque triangle on pouvait faire correspondre un cercle, le cercle circonscrit, dont il a proposé une construction générale.
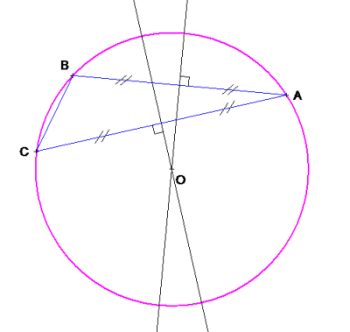
- Il a démontré qu'un triangle isocèle avait deux angles de même mesure.
- Il affirme aussi qu'un triangle est déterminé si la base et les angles à la base sont donnés.
- Thalès propose en outre le "fameux Théorème de Thalès" qui lui permit de mesurer la pyramide de Kheops.
La première démonstration de ce théorème est cependant à attribuer à Euclide (4e-3e av. J.-C.) qui la présente dans ses "Éléments", à la proposition 2 du livre VI.
7. Thales et son voyage en Egypte
Thalès partit un jour pour l' Égypte. Il pénétra dans le lac Maréotis et s'embarqua sur une felouque afin de remonter le Nil. Après quelques jours de voyage il aperçut, dressée au milieu d'un large plateau, la pyramide de Kheops. Les dimensions du monument âgé alors de 2 000 ans, dépassaient de loin tout ce qu'il avait imaginé.

Comment mesurer cette pyramide ?
Thalès regardant son ombre eut alors cette idée :
"Le rapport que j'entretiens avec mon ombre est le même que celui que la pyramide entretient avec la sienne."
Il en déduisit ceci :
" à l'instant où mon ombre sera égale à ma taille, l'ombre de la pyramide sera égale à sa hauteur."
Voici l'idée lumineuse de Thalès.
 |
 |
Un problème cependant se pose.
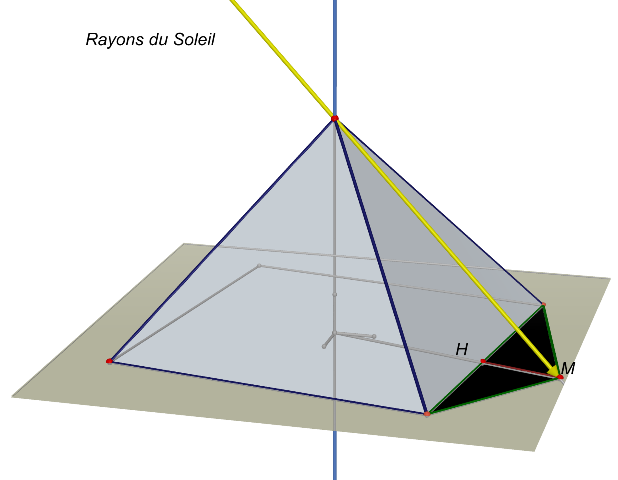
Thalès ne peut mesurer concrètement que la partie de l'ombre de la pyramide extérieure à la base. A première vue on se dit qu'il faut simplement rajouter à cette distance le 1/2 côté de la pyramide.
Cependant, la plupart du temps, le triangle noir (de hauteur (HM) est quelconque et la mesure est impossible.
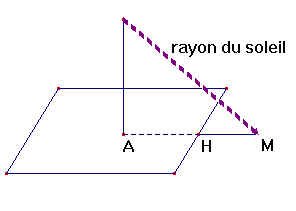
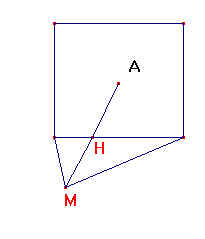
En général, la partie AH est inaccessible puisque située à l'intérieure de la base de la pyramide. Cependant, lorsque (HM) est perpendiculaire au côté de la base de la pyramide, tout est plus simple.
Dans ce cas, AH=côté/2 et l'application du théorème de Thales est aisée.
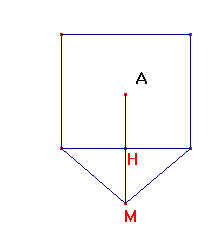
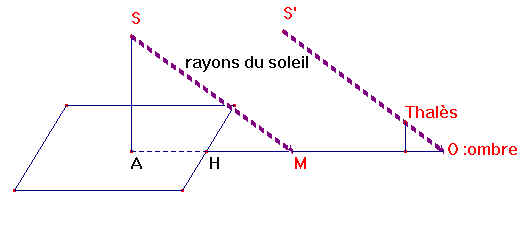
Il faut donc que :
-
- l'ombre soit perpendiculaire au côté (cela arrive au moment où le soleil est à son zénith, soit à midi)
- et que cette ombre soit visible ( i.e. pas située à l'intérieure de la pyramide)
Selon les astronomes, cela n'est possible que 2 jours dans l'année, le 21 novembre ou le 20 janvier !!!!!
8. Sa mort en 547 av. J.C.
Quelques légendes accompagnent sa vie, la plus connue est celle où, un soir qu'on le conduisait hors de sa demeure pour observer les étoiles, il tomba dans un trou et que la femme qui l'accompagnait se moqua de lui en lui disant :
"Eh bien Thalès, tu n'es pas capable de voir où tu mets les pieds et tu prétends connaître les choses du ciel !"
Pour d'autres, il est mort de déshydratation en regardant un concours gymnique et sur son tombeau fut inscrite cette épitaphe :
"Ce tombeau est certes étroit, mais considère qu'elle atteint les dimensions du ciel,
La gloire de Thalès, l'homme très sensé."
Bibliographie
- [Guedj1] : Denis GUEDJ, Le théorème du perroquet, Seuil. p35 et 52.
- [Singh ] : Simon Singh, Le dernier théorème de Fermat, JC Jattès.
- [Audi] : J.L.AUDIRAC, Vie et œuvre des grands mathématiciens, Magnard, Paris, 1990.




