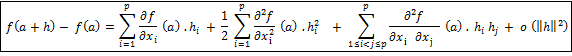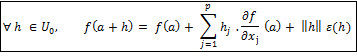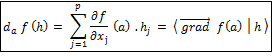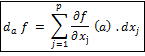Calcul différentiel et dérivées partielles.
I - Approche historique.
Approche historique :
L'étude des fonctions de plusieurs variables commence au 18e siècle mais ses fondements solides ne sont posés qu'au début du 20e siècle.
La notion de dérivée partielle est connue à la fin du 17e siècle, mais les premières équations aux dérivées partielles n'apparaissent qu'à partir de 1740 dans des problèmes de mécaniques. [Dieudo] p 43
Pour des compléments : ⇒ Approche historique sur les fonctions de plusieurs variables et la notion de dérivées partielles.
Cours sur le calcul différentiel et les dérivées partielles. (format PDF)
Pour alléger les écritures, on considérera toujours f une fonction définie sur U, un ouvert de IRp et à valeurs dans IRn, a est un vecteur de U,
![]()
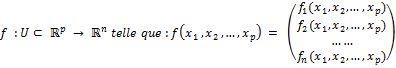
1 – Dérivées partielles.
f admet une dérivée partielle première ( dp1) en a ∈ IRp par rapport à xj, si la limite suivante existe :
![]()
![]()
- Remarque importante :
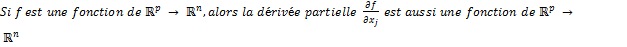 .
.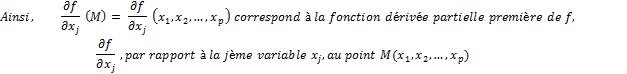
- Propriétés.
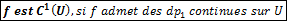 .
.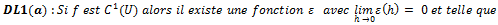 :
:
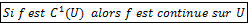 .
.
2 – Dérivées secondes.
![]() .
. ![]()
3 – Différentielles.
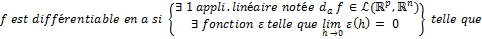 :
:
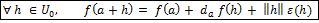
Propriétés.
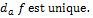
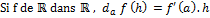 .
.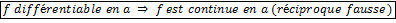 .
.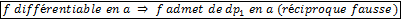 .
.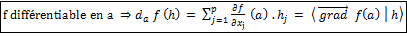
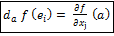
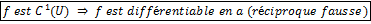 .
.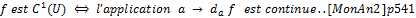
(Avant on nommait fonction continûment différentiable une fonction C1)
4 - Bilan

5 - Différentielles de fonctions C1.
- f est C1(U) ⇒
- On note pj la projection définie par : pj(h) = hj (application linéaire), alors :
da pj = pj = dxj (notation car indépendant de a),
- Jacobien : de JACOBI Carl Gustav Jacob (1804-1851)
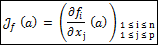
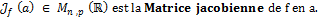 ,
,
Le jacobien de f en a est le déterminant de cette matrice. - Composition d’applications C1.
![]()
![]()
![]()
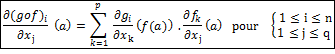
6 – Exemples importants
- Fonctions linéaires :
f linéaire L(IRn, IRp) ⇒ f est C1 et daf = f
Par exemple, la fonction linéaire Trace, est différentiable et : dA tr = tr.
- Fonctions bilinéaires :
f bilinéaire de IRp× IRn dans F ⇒ f est différentiable et pour h=(h1,h2) et a(a1,a2)
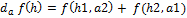
Par exemple, Le produit scalaire, le produit vectoriel sont différentiables. - Fonctions usuelles.
- Si f de IR dans IR ,
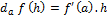
- Racine carrée sur IR+ :
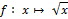 ,
, 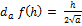 (h ∈ IR et a ∈ IR+ )
(h ∈ IR et a ∈ IR+ )
- Si f de IR dans IR ,
- Application norme. sur E espace euclidien (donc de dim. finie).
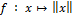
est différentiable en tout x ≠ 0 de E (non différentiable en 0) et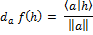
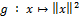
est différentiable en tout x de E et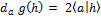
- Matrices. (consultez aussi la page sur l'histoire de la notion de matrice)
- Carrée.
f : Mn(IR) dans Mn(IR) telle que f(A) = A² est différentiable sur Mn(IR) et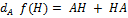
- Déterminant.
f : Mn(IR) dans IR telle que f'A) = det(A) est différentiable sur Mn(IR)
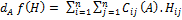
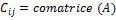
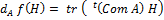
Inverse..
f : GLn(IR) dans Mn(IR) telle que f(X) = X-1 est différentiable sur GLn(IR)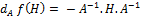
- Carrée.
7 – Compléments : Taylor- Young ordre 2.
Taylor Young ordre 2 : TAYLOR Brook (1685-1731) et YOUNG William Henry (Londres 1863 - Lausane (Suisse) 1943
![]()