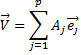Les Formes Différentielles.
Approche historique.
L'étude des fonctions de plusieurs variables commence au 18e siècle mais ses fondements solides ne sont posés qu'au début du 20e siècle.
La notion de dérivée partielle est connue à la fin du 17e siècle, mais les premières équations aux dérivées partielles n'apparaissent qu'à partir de 1740 dans des problèmes de mécaniques. [Dieudo] p 43
Pour des compléments : ⇒ Approche historique sur les fonctions de plusieurs variables et la notion de dérivées partielles.
COURS. (Version PDF)
![]()
1 - Définitions.
1a : ω est une forme différentielle sur U.Sur IR².
ω application de U → L( IR², IR) telle qu ’il existe P, Q, de classe C1 de U → IR tel que : ω(x,y) = P(x,y) dx + Q(x,y) dySur IR3.
ω application de U → L( IR3, IR) telle qu ’il existe P, Q, R de classe C1 de U → IR tel que : ω(x,y) = P(x,y) dx + Q(x,y) dy + R(x,y) dz
1b : ω est une Forme différentielle exacte (ou admettant des primitives ou totale).
ω exacte sur U ssi il existe F : U → IR de classe C1(U) telle que pour a de U : da F= ω(a)
Sur IR² : Cela correspond à :
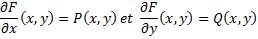
1c. Potentiel scalaire. : Soit F champ de vecteur de classe C1 sur IR3
F dérive d’un potentiel scalaire (ou admet)
si il existe un champ scalaire f de U ⊂ IR3 → IR , de classe C1, tel que :
A toute forme différentielle :
On peut associer le champ de vecteurs
Alors
1d : ω est une Forme différentielle fermée.
Sur IR² : ω fermée si :
Sur IR3 : ω fermée si :
Sur IRp : ω fermée si :
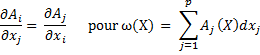
1e : Partie étoilée.
- X étoilé par rapport à A si : ∀M∈X on a [AM] ⊂ X
- X étoilé si : ∃ A∈X tq X étoilé par rapport à A.
Remarque : toute partie convexe est étoilée par rapport à chacun de ses points
2 - Théorèmes. U ouvert de IRp
2a : Proposition.
Si U connexe et ω exacte ⇒ ω admet au moins une primitive F et les autres sont de la forme {F + a, a ∈IR }
2b : Théorème.
2c : Théorème de POINCARÉ. Du nom du mathématicien français POINCARÉ Jules Henri (1854-1912).
2d : Théorème.