BTS COMPTABILITE ET GESTION
1997
MATHEMATIQUES
Durée : 2
heures Coefficient : 2
- La clarté des raisonnements et la qualité de la rédaction
interviendront pour une part importante dans l'appréciation des copies.
-
L'usage des instruments de calcul est autorisé.
- Le formulaire officiel de
mathématiques est joint au sujet.
- La page annexe doit être rendue avec la
copie.
EXERCICE 1 (10 points)
Un transporteur, s'occupant de voyages organisés, achète à un instant initial t = 0, un autocar haut de gamme nécessitant un investissement initial de 1 200 milliers de francs.
PARTIE A.
Cet investissement se déprécie. Sa dépréciation cumulée, en milliers de francs, à l'instant t, mesuré en années, est notée f(t). On suppose que f est solution sur [0 ; 13] de l'équation différentielle :
(E1) : y ' + 0,086 y = 103,2 et f(0) = 0.
1° Résolution de l'équation (E1).
a) Résoudre l'équation différentielle : y ' + 0,086 y = 0.
b) Déterminer la fonction constante, solution particulière de l'équation (E1).
c) En déduire la solution générale de l'équation (E1).
d) Déterminer la solution f de (E1) qui s'annule pour t = 0.
2° Utilisation de la fonction f.
On pose f(t) = 1 200 (1 - e - 0,086 t ) pour tout réel t de l'intervalle [0 ; 13].
La courbe représentative de la fonction f est tracée dans un repère orthogonal sur la feuille annexe ; la repérer.
Unités graphiques : sur l'axe des abscisses, 1,5 cm représente 1 an ;
sur l'axe des ordonnées, 1 cm représente 100 milliers de francs.
a) Déterminer graphiquement au bout de combien d'années l'investissement aura perdu 60 % de sa valeur ; faire apparaître sur l'annexe les tracés qui permettent d'obtenir la réponse.
b) Retrouver le résultat précédent en résolvant dans
l'intervalle [0 ; 13] l'inéquation f(t) ³ 720.
PARTIE B.
On estime que les recettes cumulées (en milliers de francs) procurées par l'exploitation de cet autocar, tous frais déduits, hors dépréciation du véhicule, sont données à l'instant t réel de l'intervalle [0 ; 13] par :
g(t) = 900 (5 + t - 5 e 0,1 t ).
1° a) Calculer la dérivée g' de g ; étudier son signe sur [0 ; 13] et construire le tableau de variation de la fonction g.
b) En déduire que les recettes cumulées sont maximales pour une valeur t0 de t dont on donnera la valeur exacte puis une valeur approchée arrondie à 1 près.
c) En utilisant la courbe représentative de la fonction g, à repérer sur l'annexe, recopier et compléter le tableau de valeurs suivant où l'on arrondira g(t) à l'entier le plus proche.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| g(t) | 1126 | 1532 | 359 |
2° A tout instant, la différence g(t) - f(t) représente l'exploitation e(t) de l'autocar. Utiliser le graphique et les tableaux de valeurs de f et de g pour répondre aux questions suivantes :
a) Au cours de quelle année l'exploitation de cet autocar est-elle la plus profitable ?
b) Au cours de quelles années l'exploitation de cet autocar conduit-elle à un déficit ?
EXERCICE 2 (10 points)
Une compagnie bancaire dont la clientèle est très nombreuse propose des placements d'argent sous forme de produits financiers. L'objet de cet exercice est d'étudier deux types de placements.
Tous les résultats numériques seront donnés à 10 - 3
près.
Etude d'un produit de type A.
La banque constate que le produit de type A a intéressé 10 % de sa clientèle.
1° Un sondage est effectué auprès d'un échantillon aléatoire de 10 clients de la banque. Soit X la variable aléatoire prenant pour valeurs le nombre de clients d'un tel échantillon ayant choisi le produit A.
a) Préciser la loi de probabilité suivie par X. Justifier. Donner les valeurs des paramètres.
b) Calculer la probabilité pour qu'au moins deux clients de l'échantillon aient choisi le produit A.
c) Montrer que la probabilité pour que moins de 5 clients de l'échantillon aient choisi le produit A, sachant que deux clients au moins en sont déjà détenteurs, est de 0,994 à 10 - 3 près.
2° Un sondage est maintenant effectué auprès d'un échantillon aléatoire de 30 clients de la banque. Soit encore X la variable aléatoire prenant pour valeurs le nombre de clients d'un tel échantillon ayant choisi le produit A.
a) Préciser la loi de probabilité suivie par X. Déterminer le nombre moyen de produits A choisis.
b) On approche la loi de X par une loi de Poisson ; préciser son paramètre.
c) En utilisant cette approximation, calculer la
probabilité qu'au moins deux clients de l'échantillon aient choisi le
produit A.
Etude d'un produit de type B.
La banque décide de proposer un produit de type B.
Soit Z la variable
aléatoire qui, à tout échantillon de taille n, associe le pourcentage p des
clients de l'échantillon intéressés par ce produit.
On décide d'assimiler la loi de Z à la loi normale 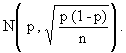
Un sondage auprès d'un échantillon aléatoire de 100 clients a montré que 80 personnes sont intéressées par le produit B.
1° Dans le cas où n = 100 :
a) Estimer p.
b) Estimer l'écart type de la population.
2° Déterminer la taille n d'un échantillon où n
³ 30 pour que l'intervalle de confiance de p soit
[0,702 ; 0,898] avec le coefficient de confiance 95 %.
Annexe :
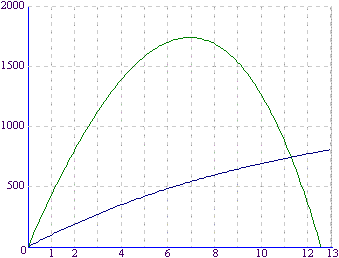
(le jour de l'examen le graphique
ci-dessus
était fourni sur papier
millimétré)
|
t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
f(t) |
0 |
99 |
190 |
273 |
349 |
419 |
484 |
543 |
597 |
647 |
692 |
734 |
772 |
808 |