BTS COMPTABILITE ET GESTION 1996
MATHEMATIQUES
Durée : 2 heures       Coefficient : 2

- La clarté des raisonnements et la qualité de la rédaction interviendront pour une part importante dans l'appréciation des copies.
- L'usage des instruments de calcul est autorisé.
- Le formulaire officiel de mathématiques est joint au sujet.

EXERCICE 1 (10 points)

Une agence immobilière envisage de commercialiser un programme de construction d'appartements. Deux projets lui sont soumis :

Projet P₁ : Le coût de production de n appartements (n entier et 2 £ n £ 20) est donné en millions de francs (MF) par : 

f(n) = ln (3,2 n + 1).

Projet P₂ : Le coût de production de n appartements (n entier et 2 £ n £ 20) est donné en millions de francs (MF) par : 

g(n) = ln (0,4 n² + 1).

Dans les deux cas le prix de vente envisagé pour un appartement est de 500 000 F soit 0,5 MF. Le chiffre d'affaires prévisible pour les ventes de n appartements est donc h(n) = 0,5 n.

A-  Etude théorique

1° a)  Calculer la dérivée f ' de la fonction f définie sur [2 ; 20]  par  f(x) = ln (3,2 x + 1).
En déduire le tableau de variation de f sur [2 ; 20].

b) Calculer la dérivée g' de la fonction g définie sur [2 ; 20] par g(x) = ln (0,4 x² + 1).
En déduire le tableau de variation de g sur [0 ; 20].

c)  Donner dans un tableau les valeurs décimales approchées à 10 ^{- 2} près des images par f et g des entiers 2, 4, 6, 9, 12, 15, 20.

2°  Tracer avec soin, sur le même graphique, les courbes représentatives des fonctions f, g, h, où pour tout élément x de [2 ; 20],   h(x) = 0,5 x.

Unités graphiques : 1 cm sur l'axe des abscisses, 2 cm sur l'axe des ordonnées.

B -  Retour au problème concret

Le nombre d'appartements commercialisés est nécessairement un entier entre 2 et 20.

1°  Utiliser le graphique précédent pour :
  a) Déterminer le nombre d'appartements correspondant au même coût de production pour les deux projets.
  b)  Déterminer le nombre maximum d'appartements dont on peut envisager la construction pour chacun des deux projets si le coût de production est limité à 3,6 MF.

2°  Retrouver par le calcul les résultats du 1a) et du 1b).

3°  Pour chaque projet, le bénéfice réalisable par l'agence est égal, pour les ventes de n appartements, au chiffre d'affaires diminué du coût de production.

  a)  Exprimer en fonction de n les bénéfices B₁(n) et B₂(n) réalisables par l'agence avec respectivement les projets P₁ et P₂.
  b)  Calculer les valeurs décimales approchées à 10 ^- 2 près de B₁(6), B₂(6), B₁(10), B₂(10).
Comparer la rentabilité des projets P₁ et P₂.

4°  En utilisant les représentations graphiques et les calculs qui précèdent pour n ³ 6
  a)  Préciser, selon les valeurs de n, le projet garantissant à l'agence le bénéfice le plus élevé.
  b)  Préciser, pour chaque projet, les valeurs de n pour lesquelles le bénéfice est au moins égal à 3 MF.

 

EXERCICE 2 (10 points)

L'objet de l'exercice est l'étude de différents aspects du fonctionnement d'une entreprise de prêt à porter.

Les parties A, B, C sont indépendantes.

Les résultats définitifs seront donnés sous forme de valeur décimale approchée à 10 ^- 2 près.

A -  Le service qui gère les commandes a relevé pour les années passées une moyenne de 5 erreurs pour 100 commandes.

On suppose que la variable aléatoire X qui mesure le nombre d'erreurs pour 100 commandes suit la loi de Poisson de paramètre 5.

1°  Déterminer la probabilité de dénombrer pour une série de 100 commandes :
    a)  5 erreurs exactement.
    b)  moins de 5 erreurs.
    c)  au moins 5 erreurs.

2°  Déterminer le plus petit entier k tel que la probabilité d'avoir moins de k erreurs soit supérieur à 0,9.

B -  A l'atelier de coupe, deux machines M₁ et M₂ découpent les pièces ; celles-ci sont stockées sans distinction de provenance.

La machine M₁ découpe 60 % des pièces ; 5 % de ces pièces sont défectueuses.
La machine M₂ découpe 40 % des pièces ; 2,5 % de ces pièces sont défectueuses.

On notera E₁ l'événement " la pièce a été découpée par la machine M₁ ".
On notera E₂ l'événement " la pièce a été découpée par la machine M₂ ".
On notera D l'événement " la pièce est défectueuse ".

1°  On prélève au hasard une pièce de la production totale.
  a)  Quelle est la probabilité de prélever une pièce défectueuse provenant de M₁ ?
  b)  Quelle est la probabilité de prélever une pièce défectueuse provenant de M₂ ?
  c)  En déduire que la probabilité de prélever une pièce défectueuse est 0,04.

2° On prélève une pièce, on s'aperçoit qu'elle est défectueuse. Calculer la probabilité qu'elle provienne de M₁.

3° A la sortie de l'atelier de coupe on prélève au hasard, successivement et avec remise, 10 pièces.
Quelle est la probabilité d'avoir au plus 2 pièces défectueuses ?

C - Les pièces bien découpées alimentent l'atelier de couture où elles sont assemblées. Les articles ainsi obtenus subissent un contrôle à la sortie de cet atelier. Pour apprécier la qualité de la production, le contrôleur cherche à évaluer le pourcentage p d'articles non commercialisables. Pour cela, il prélève au hasard et avec remise des échantillons de taille n, cette taille étant petite devant la production totale.

On suppose que la variable aléatoire F qui, à tout échantillon, associe le pourcentage d'articles non commercialisables, suit la loi norm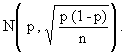ale  où p est le pourcentage inconnu d'articles non commercialisables dans la production totale.

1°  Le contrôleur prélève un échantillon de 125 articles et constate que 10 ne sont pas commercialisables.
  a)  Déterminer le pourcentage f d'articles non commercialisables de cet échantillon.
  b)  Déterminer une estimation de p, par intervalle de confiance centré en f , avec le coefficient de confiance 95 %.

2°  Quelle doit être la taille minimale n (n est un nombre entier) de l'échantillon prélevé pour que, avec le coefficient de confiance 95 %, le pourcentage p soit de 8 % à 2 % près ?

---