EUCLIDE de Samos

Sommaire

1. Euclide, personnage mystérieux.
2. Les Eléments, approche historique et historicité.
   1. Les Eléments, un texte apocryphe.
   2. La première oeuvre imprimée.
   3. Vers un souci de rigueur historique : Le codex Vaticanus.
3. Les Eléments.
   1. Description de l'ouvrage.
   2. Le premier Livre.
      1. Définitions.
      2. DEMANDES ou POSTULATS.
      3. Le 5ème Postulat d'EUCLIDE et les géométries non euclidiennes.
      4. Notions communes.3b5. Les propositions du livre I des Eléments d'EUCLIDE.
   3. Le Livre II.
4. Qu'est-ce qu'un point, qu'une droite, qu'un nombre pour EUCLIDE ?
5. Quelle nuance entre postulat et axiome ?
6. Qu'est-ce qu'une construction en mathématique au sens d'Euclide ?
7. La division euclidienne

 

---

 1. Euclide, personnage mystérieux

La personnalité d'Euclide nous est quasiment inconnue.

• Proclus de Lycie, dit « le Diadoque » (littéralement, "celui par qui le sceptre est transmis"), vécut au 5ème siècle, sans doute de 412 à 485. Né à Byzance (Constantinople), il étudia à Alexandrie, Aristote (4ème av. JC) et les mathématiques, puis à l'Académie d'Athènes. Néoplatonicien, il accède à la tête de l'institution (et devient « le diadoque »).
  Proclus de Lycie affirme, au 5ème siècle après J.-C. :

qu'« Euclide n'est pas beaucoup plus jeune que les mathématiciens du 4ème siècle avant J.-C. », et qu' « en rassemblant des Eléments, il en a coordonné beaucoup d'Eudoxe (5ème av. JC), perfectionné beaucoup de Théétète (4ème av. JC) et évoqué dans d'irréfutables démonstrations ceux que ses prédécesseurs avaient montrées de manière relâchée ..(..) Euclide est plus récent que les disciples de Platon(4ème av. JC) mais plus ancien qu'Archimède (3ème av. JC) et qu'Eratosthène (3ème av. JC) .. ». [2] page55

Euclide aurait donc vécu au 3ème siècle avant J.-C., à Alexandrie où il y aurait enseigné la géométrie dans ce que certains appellent l'école de mathématiques de l'université d'Alexandrie.

• Remarque : Euclide est aussi cité par Pappus (6ème ap. JC) qui prend sa défense, suite à une critique d'Appolonius de Perge (Perge 262 - Alexandrie 190 env.) portant sur une étude de lieu géométrique figurant dans les coniques.

Les Eléments (13 livres), les Données, la Division des figures, les Phénomènes et l'Optique, sont autant d'ouvrages qui lui sont attribués et qui nous sont tous parvenus.
On compte aussi "une Catoptrique" (géométrie des rayons réfléchis), et "une introduction harmonieuse", ouvrages qui portent son nom mais dont l'origine semble douteuse.
On connaît une version arabe de son traité sur la division des figures et Pappus (6ème ap. JC) signale trois ouvrages sur les Porismes, les Lieux à la surface, et quatre livres sur les coniques, ces derniers étant à nos jours tous perdus.

Euclide avec un compas dans "l'Ecole d'Athène de 'Stanze di Raffaello' au Museus Vaticans.

2. Les Éléménts : Approche historique et historicité

---

2.a. Les Éléments, un texte apocryphe

Le texte des Eléments n'existe pas et ces derniers ne nous sont connus que de façon apocryphe.
On ignore en outre si les 13 livres que constituent les Eléments (il semble avéré que les livres 14 et 15 sont des additions plus tardives) sont le fait du travail du seul Euclide ou d'un groupe constitué autour de lui.
Cependant la citation de Proclus de Lycie (411 - 487) citée précédemment, semble indiquer qu'ils résultent en partie du rassemblement de travaux antérieurs.

Les Éléments constituent le plus ancien exemple d'ouvrage traitant de mathématiques axiomatisées, et la première oeuvre rédigée dans un souci de rigueur scientifique et logique. Cela lui confère une place à part dans la littérature scientifique et explique sa notoriété mondiale.

2.b. La première oeuvre imprimée.

Les Éléments furent l'une des premières oeuvres imprimées (à Venise en 1482) et seule la Bible compte plus d'éditions publiées. (On dénombre plus de 1 000 éditions des Éléments).
L'italien Niccolo Tartaglia (1500 ?-1557), célèbre pour ses travaux sur la résolution d'équations de degré 3, propose une édition publiée à Venise en 1543.

2.c. Vers un souci de rigueur historique : Le codex Vaticanus.

Cependant peu de traductions sont fidèles au texte grec.

« Peu d'ouvrages ont été aussi souvent traduits, commentés et reproduits que les Éléments d'Euclide, mais il n'est pas d'auteurs avec qui ses traducteurs aient pris d'aussi étranges libertés [...] », 
déclarent Lagrange (1736 - 1813) et Delambre (1749 - 1822).

Les anciennes traductions de références sont la version latine du Commandin (1509-1575) de 1572 et la version grecque du Princeps de Bâle de 1533.

Jusqu'au début du 19ème siècle, la partie purement géométrique des Éléments était restée, soit un ouvrage d'enseignement - en Angleterre en particulier - soit un ouvrage de référence et un modèle que l'on suivait dans ses grandes lignes.
Certains même, notamment en France au 17ème siècle, éditaient des ouvrages d'Euclide vulgarisés.

En Angleterre, la tradition grecque imposait plus de rigueur. L'ouvrage de Robert Simson (1687 - 1768) en est le plus célèbre exemple tout en en symbolisant les limites. La traduction est, malheureusement pour les historiens des sciences, mathématiquement bien plus rigoureuse que l'originale.
C'est aussi avec ce souci de rigueur que travaille le français François Peyrard (1760 - 1822) en 1804 et en 1809 un peu avant d'entrer dans l'histoire des sciences.

Ce dernier déclare dans la préface à sa traduction :

" Lorsque je fus nommé Bibliothécaire de l'Ecole Polytechnique, je formais le projet de donner au public une traduction littérale des Oeuvres d'Euclide et d'Archimède (286 av. JC - 212 av. JC), les deux plus grands Géomètres de l'antiquité. Je pensois qu'il étoit en quelque sorte de mon devoir de consacrer mes moments de loisir à des travaux qui fussent analogue à ceux de l'Ecole Polytechnique."

Peyrard (1760 - 1822) s'occupe en 1814 de répertorier le butin que Napoléon (1769-1821) ramenait du Vatican. Il fait alors une découverte de renommée mondiale en identifiant le manuscrit d'Euclide connu sous le nom de "Vaticanus graecus 190", version la plus ancienne du célèbre géomètre grec.
Ce manuscrit qui est daté du 10ème siècle provoque le réveil des philologues et épistémologistes qui prennent le dessus sur les mathématiciens. Ils préoccupent désormais de l'histoire de la reconstitution ,aussi précise que possible, du plus célèbre texte mathématique de l'histoire.

La version actuelle la plus fidèle au "manuscrit 190" est celle dite Heiberg-Menge, (grâce aux travaux de J.L. Heiberg (1854-1928), T.L.Heath, P.Tannery et autres historiens des mathématiques). Éditée en grec et en latin àLeipzig à partir de 1882, elle fait encore autorité de nos jours et est la base de la célèbre traduction de Sir Thomas Little Heath (1841 - 1940).

Cependant, c'est l'édition de F.Peyrard (nouveau tirage de 1993) qui reste assez proche de celle de Heiberg qui servira de base à l'étude qui va suivre.

3. Les Éléments : Description

---

3.a. Description des Eléments

Les manuscrits des Éléments se répartissent en deux classes :

Ceux qui sont liés à la version de Théon d'Alexandrie (4 e siècle) qui édita et commenta les Éléments. On en compte plusieurs du Xe, XI e et XIIe siècle.Ceux qui présentent une version antérieure à celle de Téon, comme le manuscrit Codex Vaticanus, Gr. 190 du Xe siècle, découvert par Peyrard en 1808, (les plus anciennes sources sont des papyrus du IIIe et IVe siècle).

Les Éléments se composent de 13 livres qui abordent des thèmes mathématiques assez variés, regroupant toutes les connaissances mathématiques de l'époque
On ne peut cependant pas considérer les Éléments comme une simple compilation.
EUCLIDE classe les propositions dans un ordre logique, fait montre de beaucoup de rigueur et expose des résultats nouveaux.

Les livres I à IV traitent de la géométrie plane.

• Le Livre I : Ce livre est précédé des définitions des entités géométriques utilisées par la suite.
  EUCLIDE définit la notion de points, de ligne, de segments. Ces définitions sont suivies de cinq demandes ou postulats, puis des notions communes ou axiomes.
  C'est dans ce livre qu'EUCLIDE propose la première démonstration de l'histoire du fameux théorème de Pythagore (propositions 47 et 48).
  
  
• Le livre II s'inspire des résultats attribués à l'Ecole pythagoricienne relatifs à l'algèbre géométrique.
  EUCLIDE démontre géométriquement les développements désormais classiques : (a+b)² = a² + 2ab + b² ; a(b+c+..) =ab + ac + ...
  Le produit ab étant interprété comme l'aire d'un rectangle de côtés a et b.
  EUCLIDE considèrera toujours que les nombres sont associés à des grandeurs : longueurs de segments, aires et volumes. On additionne donc des nombres (de même nature) en mettant bout à bout des segments.
  
  
• Le livre III traite de la géométrie du cercle.
  
  
• Le livre IV est consacré aux polygones, à leur construction (à la règle et au compas) et à leur inscription dans un cercle. Ces résultats semblent être inconnus des pythagoriciens et les historiens les attribuent souvent aux sophistes, membres de la première grande école athénienne au 5ème siècle av. J.-C.
  
  
• Le livre V est d'un niveau mathématique bien supérieur.
  Il traite de la théorie des proportions et est communément attribué aux travaux d'EUDOXE (vers 400 av. J.-C. - vers 347 av. J.-C.).
  
  Si les pythagoriciens avaient aussi développé une théorie des proportions, celle-ci ne s'appliquait qu'aux grandeurs commensurables (c'est à dire aux fractions, pas à √2 par exemple).
  
  EUCLIDE élargit le champ d'application de cette théorie. Celle-ci sera même reprise, dans ses grandes lignes, par le célèbre mathématicien allemand WEIERSTRASS Karl Theodor Wilhelm (1815-1897), reformateur de l'analyse au 19ème siècle.
  
  
• Le livre VI applique cette théorie des proportions entre grandeurs à la géométrie plane.
  
  C'est à la proposition 2 du livre VI, qu'EUCLIDE démontre le fameux théorème dit de THALES.
  
  
• Le livres VII, VII et IX sont consacrés à la théorie des nombres (entier supérieur à 2 bien sur), que l'on nomme maintenant arithmétique.
  
  Dans le livre VII, il expose l'algorithme qui porte son nom (l'algorithme d'EUCLIDE), et qui permet de trouver le PGCD de deux entiers. Il l'utilise pour prouver que deux nombres sont premiers entre eux.
  
  Le livre VIII porte sur les proportions et les progressions géométriques.
  
  Dans Le livre IX, on trouve à la proposition 20, la démonstration par l'absurde de l'existence d'une infinité de nombres premiers. (voir la page nombres premiers pour cette démonstration).
  EUCLIDE y expose aussi une ébauche de démonstration du théorème de décomposition d'un entier en facteurs premiers (⇒ le théorème fondamental de l'arithmétique), et donne l'expression de la somme de termes consécutifs d'une suite géométrique.
  
  Il démontre aussi qu'un nombre de la forme 2^n-1(2ⁿ -1) est parfait quand 2ⁿ - 1 est premier.
  
  
• Le livre X utilise presque tout ce qui a été démontré dans les livres précédents pour étudier les lignes commensurables ou incommensurables entre elles. Il est considéré comme l'un des plus subtils.
  
  EUCLIDE y démontre géométriquement les relations du type :

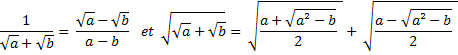
• Le Livre XI : La stéréométrie, c'est à dire l'étude des propriétés des solides élémentaires est l'objet du livre XI.
  
  
• Le livre XII présente la méthode dite « d'exhaustion » (cf. rem), sorte de méthode d'intégration reprise aussi par Archimède, et qui permet d'établir des résultats sur la mesure du cercle, de la pyramide, du cône et de la sphère. Ce livre est parfois aussi attribué à EUDOXE (vers 400 av. J.-C. - vers 347 av. J.-C.).
  
  
• Le livre XIII est lui consacré à la construction des cinq polyèdres réguliers avec les résultats du livre X.
  
  Proclus affirme d'ailleurs que l'objectif des Éléments était la construction des solides de Platon

Remarque :

La désignation "d'exhaustion" fut introduite à la Renaissance et est souvent considérée comme impropre.
En soustrayant de la plus grande de deux grandeurs données plus de sa moitié, et du reste plus de sa moitié, et ainsi de suite, on obtiendra (i.e. on finira par obtenir en réitérant le procédé un nombre fini de fois) une grandeur moindre que la plus petite. Ce principe dichotomique évite un délicat passage à la limite, donc l'introduction du concept d'infiniment petit ou d'infiniment grand posant autant de problèmes mathématiques que philosophiques.

La synthèse des mathématiques connues à son époque, auxquelles il apporte compléments, démonstrations et rigueur en arithmétique, algèbre et géométrie, voilà ce que représentent les Éléments.

Cette rigueur est mise en place au moyen de cinq postulats (les demandes) et de neuf axiomes relatifs aux grandeurs ("notions communes" à l'usage de la géométrie et de l'arithmétique).

3.b. Le premier livre des éléments d'Euclide

Le Livre I est précédé des définitions des entités géométriques utilisés par la suite. EUCLIDE définit la notion de points, de ligne, de segments. Ces définitions sont suivies de cinq demandes ou postulats, puis des notions communes ou axiomes.

3b1. DÉFINITIONS

1. Un point est ce dont la partie est nulle.

2. Une ligne est une longueur sans largeur.
Notons qu'EUCLIDE entend par ligne, une ligne droite ou courbe, ce que l'on nommerait aujourd'hui une partie de courbe ou une courbe si on considère qu'elle peut être infinie.
- la ligne droite ou simplement droite qui est la ligne la plus courte qui puisse exister entre deux points ;
- la ligne courbe ou simplement courbe comme les cercles, les coniques, les spirales, les hélices.

3. Les extrémités d'une ligne sont des points.
Une ligne pour EUCLIDE semble donc être finie d'après cette définition mais le postulat n°2 indique que l'on peut prolonger indéfiniment, selon sa direction, une droite finie. Alors ?
De plus, Il ne dit pas combien de points terminent une ligne, par exemple la circonférence d'un cercle n'a pas de fin.
 
4. La ligne droite est celle qui est également placée entre ses points.
Ceci est la définition d'une droite pour nous.

5. Une surface est ce qui a seulement longueur et largeur.

6. Les extrémités d'une surface sont des lignes.

7. La surface plane est celle qui est également placée entre ses droites.

8. Un angle plan est l'inclinaison mutuelle de deux lignes qui se touchent dans un plan, et qui ne sont point placées dans la même direction.

9. Lorsque les lignes, qui comprennent ledit angle, sont des droites, l'angle se nomme rectiligne.

10. Lorsqu'une droite tombant sur une droite fait deux angles de suite égaux entre eux, chacun des angles égaux est droit; et la droite placée au-dessus est dite perpendiculaire à celle sur laquelle elle est placée.

11. L'angle obtus est celui qui est plus grand qu'un droit,

12. L'angle aigu est celui qui est plus petit qu'un droit.

13. On appelle limite ce qui est l'extrémité de quelque chose.

14. Une figure est ce qui est compris par une seule ou par plusieurs limites.

15. Un cercle est une figure plane, comprise par une seule ligne qu'on nomme circonférence ; toutes les droites, menées à la circonférence d'un des points placés dans cette figure, étant égales entre elles.

16. Ce point se nomme le centre du cercle

17. Le diamètre du cercle est une droite menée par le centre, et terminée de part et d'autre par la circonférence du cercle : le diamètre partage le cercle en deux parties égales.

18. Un demi-cercle est la figure comprise par le diamètre, et la portion de la circonférence, soutendue par le diamètre.

19. Un segment de cercle est la figure comprise par une droite et par la circonférence du cercle ; le demi-cercle étant plus grand ou plus petit que le segment.

20. Les figures rectilignes sont celles qui sont terminées par des droites.

21. Les figures trilatères sont terminées par trois droites.

22. Les quadrilatères, par quatre.

23. Les multilatères, par plus de quatre.

24. Parmi les figures trilatères, le triangle équilatéral est celle qui a ses trois côtés égaux.

25. Le triangle isocèle, celle qui a seulement deux côtés égaux.

26. Le triangle scalène, celle qui a ses trois côtés inégaux.

27. De plus, parmi les figures trilatères, le triangle rectangle est celle qui a un angle droit.

28. Le triangle obtusangle, celle qui a un angle obtus.

29. Le triangle acutangle, celle qui a ses trois angles aigus.

30. Parmi les figures quadrilatères, le carré est celle qui est équilatérale et rectangulaire.

31. Le rectangle, celle qui est rectangulaire, et non équilatérale.

32. La rhombe, celle qui est équilatérale, et non rectangulaire.

33. Le rhomboïde, celle qui a ses côtés et ses angles opposés égaux entre eux, et qui n'est ni équilatérale ni rectangulaire.

34. Les autres quadrilatères, ceux-là exceptés, se nomment trapèzes.

35. Les parallèles sont des droites, qui, étant situées dans un même plan, et étant prolongées à l'infini de part et d'autre, ne se rencontrent ni d'un côté ni de l'autre.

3b2. DEMANDES ou POSTULATS.

1. Conduire une droite d'un point quelconque à un point quelconque.

2. Prolonger indéfiniment, selon sa direction, une droite finie.

3. D'un point quelconque, et avec un intervalle quelconque, décrire une circonférence de cercle.

4. Tous les angles droits sont égaux entre eux.

5. Si une droite, tombant sur deux droites, fait les angles intérieurs du même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.

3b3. Le 5ème Postulat d'EUCLIDE et les géométries non euclidiennes.

Le 5ème postulat est bien sûr le plus célèbre puisque c'est la clée de la géométrie dite euclidienne.
Au début du 19ème siècle, des géométries non euclidiennes apparurent, en n'admettant pas le cinquième postulat :

La géométrie hyperbolique sur des surfaces à courbure constante négative du Russe LOBATSCHEVSKI Nikolaï Ivanovitch (1792-1856), du Hongrois BOLYAI Jànos (1802-1860) et de l'Allemand GAUSS Carl Friedrich (1777-1855).
Cette nouvelle géométrie utilise le fait qu'il y ait une infinité de parallèles passant par un point extérieur à une droite donnée.

La géométrie elliptique sur des surfaces à courbure constante positive de l'Allemand G. F. B. Riemann (1826-1866).
Dans cette géométrie, il n'existe aucune droite parallèle à une droite donnée passant par un point extérieur à cette droite.

3b4. NOTIONS COMMUNES.

1. Les grandeurs égales à une même grandeur, sont égales entre elles.

2. Si à des grandeurs égales, on ajoute des grandeurs égales, les touts seront égaux.

3. Si de grandeurs égales, on retranche des grandeurs égales, les restes seront égaux.

4. Si à des grandeurs inégales, on ajoute des grandeurs égales, les touts seront inégaux.

5. Si de grandeurs inégales, on retranche des grandeurs égales, les restes seront inégaux.

6. Les grandeurs, qui sont doubles d'une même grandeur, sont égales entre elles.

7. Les grandeurs, qui sont les moitiés d'une même grandeur, sont égales entre elles.

8. Les grandeurs, qui s'adaptent entre elles, sont égales entre elles.

9. Le tout est plus grand que la partie.

3b5. Les propositions du livre I des Eléments d'EUCLIDE.

• • Les cas d'égalité des triangles.Proposition 4, 8, 26.
  • La somme des mesures des angles d'un triangleProposition 32.
  • La construction du carré.Proposition 46.
  • Le Théorème de Pythagore.Proposition I-47 des Éléments d'Euclide, théorème directProposition I-48 des Éléments d'Euclide, théorème réciproque

3.c. Le livre II

• Le livre II est composé de 2 définitions et 14 propositions (12 théorèmes et 2 problèmes) qui ne diffèrent pas selon les éditions .
• Il utilise les derniers résultats du livre I et en prolonge certains en particulier la résolution de la quadrature des figures rectilignes ou polygones (prop.14 ).
• Les propriétés 1 à 10 furent souvent interprétées algébriquement car elles traitent d'équivalences entre des aires rectangulaires.
• Elles n'ont pas d'enchaînement déductif évident. Par exemple, seule la Prop.4 est réutilisée dans les Porp. 5, 6, 7 et 8 et les démonstrations de ces 10 propriétés utilisent surtout des résultats établis dans la dernière partie du livre I.
• La Prop. 11 est un problème qui consiste à partager une droite en extrême et moyenne raison.
• Les Prop. 12 et 13 généralisent le théorème de Pythagore aux triangles quelconques (d'angle obtu ou aigu).

4. Qu'est-ce qu'un point, qu'une droite, qu'un nombre pour EUCLIDE ?

---

Euclide débute son ouvrage par des définitions que l'on doit admettre pour faire de la géométrie dite euclidienne, ce qui est le cas au collège et au lycée.

• Q1. Peut-on tracer un point au tableau ou sur une feuille avec la définition d'Euclide ?
  Non, en fait un point n'a ni longueur, ni largeur.
  En mathématique on représente un point par l'intersection de deux lignes comme cela :  × ou +
  En fait, un point n'existe pas car on peut toujours mesurer cette intersection. On ne fait qu'en donner une représentation imagée.
  
  
• Q2. Avec nos termes actuels, que désignent la définition 2 et la définition 4 ?
  • Définition 2. Une ligne est une longueur sans largeur.
    Notons qu'EUCLIDE entend par ligne, une ligne droite ou courbe, ce que l'on nommerait aujourd'hui une partie de courbe ou une courbe si on considère qu'elle peut être infinie.
    Pour EUCLIDE, une ligne est une ligne droite ou une  courbe.
    
    
  • Définition 4. La ligne droite est celle qui est également placée entre ses points.
    Ceci est la définition d'un segment pour nous.
    
    
• Q3. Peut-on les tracer au tableau ou sur une feuille avec la définition d'Euclide ?
  Et bien non, une ligne ne doit pas avoir d'épaisseur. Or toute ligne que l'on tracera en aura une. C'est encore une image figurée que l'on représente.
  
  
• Q4 : Qu'est-ce qu'un nombre pour EUCLIDE.
  
  Pour EUCLIDE, Le produit ab est interprété comme l'aire d'un rectangle de côtés a et b.
  
  EUCLIDE considèrera toujours que les nombres sont associés à des grandeurs : longueurs de segments, aires et volumes. On additionne donc des nombres (de même nature) en mettant bout à bout des segments.

5. Quelle nuance entre postulat et axiome ?

---

• postulat : du latin postulare = demander : que l'on demande au lecteur d'accepter.axiome : du grec axioma = j'estime, je crois vrai : conduisant au sens d'irréfutable, d'évident.
  
  Le postulat est de nature plus philosophique que mathématique. Il est un principe (du latin principium = origine, commencement) de pensée, base de toute réflexion ou raisonnement valide au sens d'Aristote (384 av. J.C. - 322 av. J.C.), de Leibniz (1646 - 1716) et d'Emmanuel Kant (illustre philosophe allemand, 1724-1804, né et professeur à Königsberg, célèbre université qui "hébergea" les plus grands mathématiciens occidentaux). Le postulat doit être admis, consenti, avant toute poursuite du dialogue ou de la lecture : c'est une hypothèse de travail.
  
  En mathématiques, il apparaît dans la mise en place d'une théorie (système déductif cohérent) comme une proposition admise, que l'on ne pourra ni prouver, ni infirmer par ses propres moyens (ses théorèmes).
  
  
• Un axiome est un postulat. Mais il est de nature plus évidente. Quiconque doit, s'il en comprend l'énoncé, l'admettre sans discuter : c'est un truisme.
  
  L'axiome peut prendre l'aspect d'une définition : voilà un objet, il est ainsi défini, c'est comme cela et pas autrement et on ne discute pas. L'axiomatisation des mathématiques prend naissance avec Hilbert (1862 - 1943, en algèbre et géométrie), Kolmogorov (1903 - 1987, en probabilités), Cantor (1845 - 1918, en théorie des ensembles) et fait fureur jusqu'à la célèbre bataille de l'axiome du choix : Zermelo (1871 - 1953).

Après avoir défini les notions de point (ce dont la partie est nulle), de ligne (en tant que segment : longueur sans largeur dont les extrémités sont des points), de droite (ligne qui est également placée entre ses points), d'angle, de cercle, etc., de droites parallèles (qui prolongées indéfiniment d'un côté ou de l'autre ne se rencontrent pas), Euclide pose les fameux postulats dont le cinquième est resté LE postulat d'Euclide :

1. Étant donnés deux points A et B, il existe une droite passant par A et B;
2. Tout segment [AB] est prolongeable en une droite passant par A et B
(compte tenu du premier postulat, elle est unique)
3. Pour tout point A et tout point B distinct de A, on peut décrire un cercle de centre A passant par B;
4. Tous les angles droits sont égaux entre eux;
5. Par un point extérieur à une droite, on peut mener une parallèle et une seule à cette droite.

Nombreux sont ceux qui ont prétendu avoir démontré le cinquième postulat à partir des quatre autres (le problème est dans l'unicité et non dans l'existence). En fait, ils utilisaient alors inconsciemment une propriété équivalente. En retirant ou modifiant le cinquième postulat, on obtient les géométries dites "non euclidiennes".

Les quinze axiomes et postulats de la géométrie "euclidienne" se sont avérés insuffisants pour ladite géométrie. Certains iront jusqu'à parler de manque de rigueur, à travers des démonstrations basées sur la notion intuitive de superposition (cas "d'égalité" des triangles) induisant une idée de mouvement et d'isométries nullement définis.

Notons que Playfair (1748 - 1819), Pasch (1843-1930), Hilbert (1862 - 1943) se sont penchés sur l'axiomatique de la géométrie euclidienne.

6. Qu'est-ce qu'une construction en mathématique au sens d'Euclide ?

---

Construire une figure consiste, sauf consigne contraire, à déterminer les points qui la constituent en utilisant ces deux seuls instruments, la règle et le compas, hérités de la tradition platonicienne.

• La règle est considérée ici comme un moyen de relier deux points (déjà déterminés) entre eux. Elle sert à tracer un segment ou une droite: elle n'est donc pas graduée.
• Le compas sert à tracer des cercles dont le centre et un point sont déjà déterminés. Il servira aussi à placer un point en tant qu'intersection de deux cercles.

L'usage des règle et compas seuls dans une construction oblige à la réflexion, au raisonnement, mais il ne doit pas être obligatoire ou systématique. La soi-disant précision de ces instruments est très discutable.
A l'école, l'objectif de la construction, est d'évaluer les connaissances de l'élève sur un nouveau savoir et les propriétés géométriques remarquables de ce savoir (par exemple, construire la médiatrice d'un segment, suite à sa caractérisation). On pourrait cependant exiger l'usage des seuls règle non graduée et compas. Sinon on parlera de tracer plutôt que de construire. Et là, tous les outils sont permis.

L'usage d'une règle graduée, d'un rapporteur, d'une équerre, d'une bande de papier, voire, de nos jours, d'une calculatrice, etc., apparaîtra généralement dans les cas où la construction d'une figure n'est qu'un support visuel du problème étudié et non un objectif.

L'admiration quasi mystique de la droite et du cercle induite par Platon (427 av. JC - 348 av. JC) explique la notion de construction géométrique acceptable à l'aide du compas et de la règle seuls. Ceci fut sans doute un frein au développement des mathématiques par le biais de la géométrie euclidienne.

En effet, l'intersection d'une droite et d'un cercle fournit au plus deux points; par suite, le pendant algébrique de ce dogme de la construction se limite à l'équation du second degré et ne fournit de solutions qu'à des problèmes quadratiques, donc constructibles.
Ces problèmes de constructibilité au sens d'Euclide passionnent et hantent les mathématiciens jusqu'au 19ème siècle. La trissection d'un angle, la quadrature du cercle et duplication du cube sont les plus connus de ces fameux problèmes mathématiques non résolus.

Le français Wantzel (1814-1848) en prolongeant les travaux de Gauss (1777-1855), publie en 1837 un critère de non-constuctibilité à la règle et au compas (théorème de Gauss-Wantzel). Il met fin ainsi à 2 000 ans de recherches infructueuses en montrant l'impossibilité des trois célèbres problèmes (trissection, quadrature et duplication).

Cependant rien n'est vain dans l'histoire de l'humanité. Les mathématiciens grecs débordèrent d'imagination et de génie dans leur acharnement à résoudre les subtils problèmes que furent la duplication du cube, l'évaluation depi, la trisection de l'angle ou la quadrature du cercle. Les étude des sections coniques et la théorie des proportions par exemple furent développées dans ce but.

• Euclide, section dorée et pentagone/décagone régulier : 
  
  Les éléments d'Euclide traite des calculs fractionnaires à travers la théorie des proportions empruntée à Eudoxe (5ème av. JC), de l'arithmétique (étude des entiers naturels, divisibilité et nombres premiers, des nombres irrationnels découverts par les Pythagoriciens. Les derniers livres sont consacrés aux aires et aux volumes des configurations usuelles du plan et de l'espace, reprise des travaux d'Eudoxe (5ème av. JC) et Théétète (4ème av. JC) , avec l'étude des polyèdres réguliers (il faudra attendre Archimède (3ème av. JC) pour connaître le volume de la sphère et l'aire de sa surface).

7. La division euclidienne.

---

• Pour tout couple (a,b) d'entiers naturels non nuls, on peut écrire a = bq + r où q (quotient) et r (reste) sont des entiers naturels uniques avec la condition r < b.
  • • Exemple :
      Dans la division euclidienne de 113 par 5, le quotient est 22 et le reste est 3 : 113 = 22 × 5 + 3
      
      
• On doit à Euclide la première preuve de l'infinitude de l'ensemble des nombres premiers et de l'existence, pour tout entier naturel au moins égal à 2, d'un diviseur premier inférieur à son carré, ce qui permet la recherche de primarité.
  
  La preuve est assez simple, il montre que si l'ensemble des nombres premiers était fini, alors le nombre N constitué du produit de tous ces nombres premiers + 1 serait lui aussi premier, ce qui contredit l'hypothèse de départ.
  
  
• Algorithme d'Euclide pour la recherche du PGCD, dont la définition récursive (procédure qui fait appel à elle-même) peut s'écrire : pgcd(a,b) = pgcd(a,r) où a désigne le reste de la division de a par b (division euclidienne). Cette notion de récursion est fondamentale dans les algorithmes mathématiques (et informatiques). Elle permet des programmes de calcul très courts. L'algorithme doit posséder un point d'arrêt : ici ce serait si b = 0 alors pgcd = a.
  
  
• Le nom d'Euclide se rattache à de nombreux concepts mathématiques. Il s'agit cependant d'éviter tout anachronisme : des appellations comme distance euclidienne, plan euclidien, espace vectoriel euclidien, norme euclidienne, etc., veulent rappeler que le contexte mathématique sous-jacent est compatible avec la géométrie élémentaire de ce grand mathématicien.

---

Bibliographie

• [Euclide] : « Les œuvres d'Euclide », traduit littéralement par F. Peyrard, nouveau tirage de mars 1993, Librairie scientifique et technique, Paris, 1993.
• [DaDaPe] : A.DAHAN-DALMEDICO/J.PEIFFER, Une histoire des mathématiques, Seuil, Paris, 1986.
• A.. Jean-Paul Collette « Histoire des mathématiques », Vuibert.
• « Euclide, les Eléments » traduits du texte de Heiberg, introduction de Maurice Caveing, Paris, 1990, PUF.

Pour en savoir plus

• Le site alep0 traite les Éléments intégralement (en anglais).
• Le site NUMDAM propose une édition des Eléments d'Euclide numérisée.